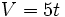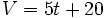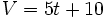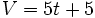Plantilla:Función afín
De Wikipedia
| Revisión de 15:38 12 dic 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 12:41 25 dic 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 26: | Línea 26: | ||
| {{Video_enlace_abel | {{Video_enlace_abel | ||
| |titulo1=Ejercicio 1 | |titulo1=Ejercicio 1 | ||
| + | |duracion=14'17" | ||
| + | |sinopsis=Representa gráficamente la función <math>y=2x+1\;</math>. | ||
| + | |url1=https://www.youtube.com/watch?v=K-C6l6tH95Q | ||
| + | }} | ||
| + | {{Video_enlace_abel | ||
| + | |titulo1=Ejercicio 2 | ||
| |duracion=6'41" | |duracion=6'41" | ||
| |sinopsis=Representa gráficamente la función <math>y=2x-41\;</math> a partir de sus puntos de corte | |sinopsis=Representa gráficamente la función <math>y=2x-41\;</math> a partir de sus puntos de corte | ||
| Línea 31: | Línea 37: | ||
| }} | }} | ||
| {{Video_enlace_aprendopolis | {{Video_enlace_aprendopolis | ||
| - | |titulo1=Ejercicio 2 | + | |titulo1=Ejercicio 3 |
| |duracion=9'10" | |duracion=9'10" | ||
| |sinopsis=Representa gráficamente las funciones: | |sinopsis=Representa gráficamente las funciones: | ||
Revisión de 12:41 25 dic 2017
Una función lineal es aquella cuya expresión analítica puede expresarse como:
 |
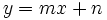es la variable independiente.
es la variable dependiente.
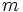es una constante que se denomina pendiente.
es otra constante denominada ordenada en el origen. (Si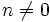 
recibe el nombre de función afín)
Representación gráfica
- La gráfica de una función lineal es una recta que corta al eje de ordenadas en el punto
.
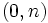- En consecuencia, para representarla, necesitamos dos puntos, uno de los cuales puede ser el
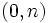. El otro punto se obtendrá a partir de la ecuación.
Ejemplo: Función lineal
- Un estanque tiene un grifo que vierte 5 litros por minuto. Haz una tabla que relacione el tiempo transcurrido (en minutos) y el volumen (en litros) de estanque que se llena. Escribe la fórmula que relaciona el volumen y el tiempo. Representa gráficamente los resultados.
- Repite el apartado anterior suponiendo que el estanque tiene un volumen inicial de 20 litros.
- ¿Y si partiésemos de un volumen inicial de 10 litros, cuáles serían los resultados?
- Compara las gráficas obtenidas e indica que tienen en común y en qué se diferencian.
- ¿Qué fórmula correspondería a esta situación gráfica?
| 1. Un estanque tiene un grifo que vierte 5 litros por minuto.
Partimos de que el estanque se encuentra vacío inicialmente. Completa la tabla:
La fórmula que expresa la relación entre el volumen y el tiempo es:
| 
|
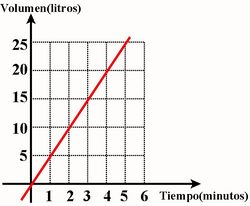
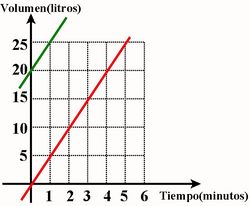
| 2. Supongamos ahora que el estanque tiene inicialmente un volumen de 20 litros.
Completa la tabla:
La fórmula que expresa la relación entre el volumen y el tiempo ahora es:
| 
|
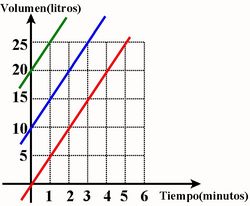
| 3. Ahora supondremos que el estanque tiene inicialmente un volumen de 10 litros.
Completa la tabla:
La fórmula que expresa la relación entre el volumen y el tiempo ahora es:
| 
|
4. Las graficas son rectas paralelas que cortan al eje de ordenadas a una altura que coincide con el volumen inicial del estanque. Por tanto, tienen en común que tienen la misma inclinación y se diferencian en el punto de corte con el eje de ordenadas.
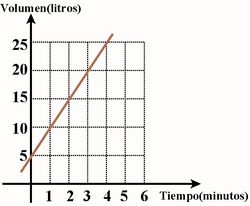
5. Para esta gráfica que corta al eje de ordenadas en 5, la fórmula que expresa la relación entre el volumen y el tiempo es:
|
|
Función lineal Descripción: En esta escena podrás ver e interactuar con las gráficas de funciones lineales y estudiar sus propiedades.
Tutorial 1 (41'50") Sinopsis:Tutorial en el que se explican los conceptos básicos y propiedades de las funciones lineales, así como su representación gráfica.
Tutorial 2 (8'23") Sinopsis: Representación gráfica de funciones lineales.
Tutorial 3: Representación con Geogebra (14'58") Sinopsis:Representación gráfica de funciones lineales con Geogebra.
Ejercicio 1 (14'17") Sinopsis:Representa gráficamente la función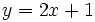 
.
Ejercicio 2 (6'41") Sinopsis:Representa gráficamente la función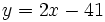 
a partir de sus puntos de corte
Ejercicio 3 (9'10") Sinopsis:Representa gráficamente las funciones:
a)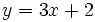 
b)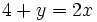 
c)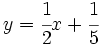 
Actividad 1a Descripción: Definición de función lineal. Ejemplos.
Actividad 1b Descripción: Actividades en las que aprenderás a representar funciones lineales y a identificar su ecuación a partir de su gráfica.
Actividad 2a Descripción: Ejercicio sobre funciones lineales.
Actividad 2b Descripción: Ejercicio sobre funciones lineales.
Actividad 2c Descripción: Ejercicio sobre funciones lineales.
Autoevaluación 1 Descripción: Identifica ecuaciones de rectas a partir de sus gráficas.
Autoevaluación 2 Descripción: Problemas sobre ecuaciones, tablas y gráficas de funciones lineales.
Autoevaluación 3 Descripción: Ejercicios sobre funciones lineales.
