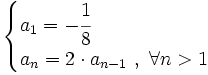Plantilla:Def progresion geometrica
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 18:00 27 dic 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 18:06 27 dic 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 14: | Línea 14: | ||
| |url1=https://youtu.be/PP8gFxUDW9M | |url1=https://youtu.be/PP8gFxUDW9M | ||
| |sinopsis=Halla el quinto término de la siguiente progresión geométrica: <math>\{ -\cfrac{3}{8}, -\cfrac{3}{2}, -6, -24, ...\}</math> | |sinopsis=Halla el quinto término de la siguiente progresión geométrica: <math>\{ -\cfrac{3}{8}, -\cfrac{3}{2}, -6, -24, ...\}</math> | ||
| + | }} | ||
| + | {{Video_enlace_khan | ||
| + | |titulo1=Ejercicio 2 | ||
| + | |duracion=2´46" | ||
| + | |url1=https://youtu.be/mM2InOlZyZk | ||
| + | |sinopsis=Una progresión geométrica tiene como término general <math>a_n=3 \cdot \left(-\cfrac{2}{3}\right)^{n-1}</math>, halla el término <math>a_5\;</math>. | ||
| + | }} | ||
| + | {{Video_enlace_khan | ||
| + | |titulo1=Ejercicio 3 | ||
| + | |duracion=4´31" | ||
| + | |url1=https://youtu.be/IE1vDZExwc4 | ||
| + | |sinopsis=Halla el término <math>a_4\;</math> de una progresión aritmética que viene dada por la siguiente ley de recurrencia: | ||
| + | :<math>\begin{cases}a_1=-\cfrac{1}{8} \\ a_n=2 \cdot a_{n-1} \ , \ \forall n>1 \end{cases}</math> | ||
| }} | }} | ||
| }} | }} | ||
Revisión de 18:06 27 dic 2017
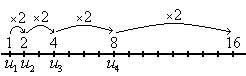
Una progresión geométrica es una sucesión de números en la que cada término se obtiene multiplicando el anterior por una cantidad fija, 
, que llamaremos razón
Por ejemplo:
es una progresión geométrica de razón r=2.
Ejercicio 1 (3´03") Sinopsis: Halla el quinto término de la siguiente progresión geométrica: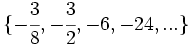 
Ejercicio 2 (2´46") Sinopsis: Una progresión geométrica tiene como término general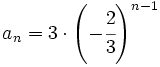 
, halla el término 
.
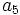Ejercicio 3 (4´31") Sinopsis: Halla el término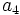 
de una progresión aritmética que viene dada por la siguiente ley de recurrencia:
Actividad 1 Descripción: Actividades en las que aprenderás el concepto de progresión geométrica y a cómo identificarlas.
Autoevaluación 1a Descripción: Extiende sucesiones geométricas.
Autoevaluación 1b Descripción: Extiende sucesiones geométricas con términos negativos y racionales.
