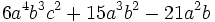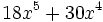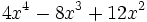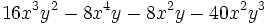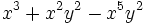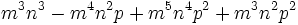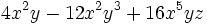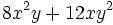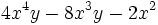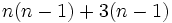Plantilla:Videos: Sacar factor común
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 10:27 15 ene 2018 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 10:32 15 ene 2018 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 181: | Línea 181: | ||
| |url1=https://youtu.be/ufZhUCXFOGE | |url1=https://youtu.be/ufZhUCXFOGE | ||
| + | }} | ||
| + | {{Video_enlace_khan | ||
| + | |titulo1=Ejercicio 5f | ||
| + | |duracion=4'40" | ||
| + | |sinopsis= | ||
| + | #Sabiendo que <math>a+b+c=7\;</math>, calcula <math>5a+5b+5c\;</math>. | ||
| + | #Sabiendo que <math>a+b+c=-1\;</math> y que <math>x+y=7\;</math>, calcula <math>-9-7x-9c-9b-7y\;</math>. | ||
| + | |||
| + | |url1=https://youtu.be/AtWAFNYsKVc | ||
| + | }} | ||
| + | {{Video_enlace_khan | ||
| + | |titulo1=Ejercicio 5g | ||
| + | |duracion=3'01" | ||
| + | |sinopsis= | ||
| + | #Sabiendo que <math>3x+3y+3z=1\;</math>, calcula <math>12x+12y+12z\;</math>. | ||
| + | #Sabiendo que <math>3a+5b=2\;</math>, calcula <math>15a+15b\;</math>. | ||
| + | |||
| + | |||
| + | |url1=https://youtu.be/jmTBC9wKMEo | ||
| }} | }} | ||
| }} | }} | ||
Revisión de 10:32 15 ene 2018
Cómo se saca factor común. Ejemplos
- En este tutorial se explica la extracción de factor común en expresiones algrebraicas, el caso más sencillo de factorización de polinomios.
- (4:40) La propiedad distributiva. Demostración geométrica.
Saca factor común:
a) 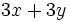
b) 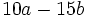
c) 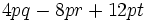
d) 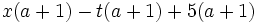
Saca factor común:
a) 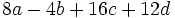
b) 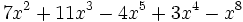
c) 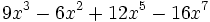
d) 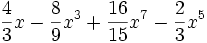
e) 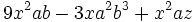
f) 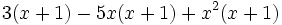
Saca factor común:
a) 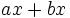
b) 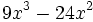
c) 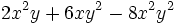
d) 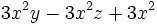
Saca factor común:
a) 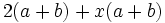
b) 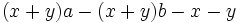
c) 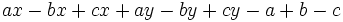
Saca factor común:
Saca factor común:
Saca factor común:
Saca factor común:
Saca factor común:
Saca factor común:
Saca factor común:
Saca factor común:
- a)
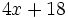
- b)
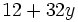
Saca factor común:
Saca factor común:
El área de un rectángulo es de 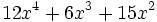 y su largo es el m.c.d. de cada uno de los sumandos del anterior polinomio. Calcula las dimensiones del rectángulo.
y su largo es el m.c.d. de cada uno de los sumandos del anterior polinomio. Calcula las dimensiones del rectángulo.
Saca factor común:
- Sabiendo que
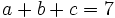 , calcula
, calcula 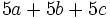 .
.
- Sabiendo que
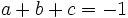 y que
y que 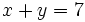 , calcula
, calcula 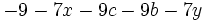 .
.
- Sabiendo que
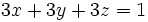 , calcula
, calcula 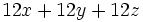 .
.
- Sabiendo que
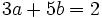 , calcula
, calcula  .
.