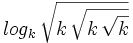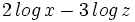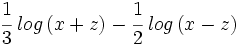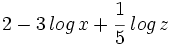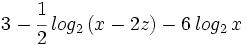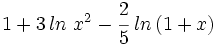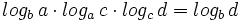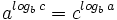Plantilla:Propiedades de los logaritmos
De Wikipedia
| Revisión de 16:30 26 sep 2018 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 75: | Línea 75: | ||
| |titulo1=Tutorial 2 | |titulo1=Tutorial 2 | ||
| |duracion=13´22" | |duracion=13´22" | ||
| - | |url1=https://www.youtube.com/watch?v=glD8VLbPqgQ&index=4&list=PL2287F157D20941E5 | + | |url1=http://www.youtube.com/watch?v=glD8VLbPqgQ&index=4&list=PL2287F157D20941E5 |
| |sinopsis=Demostración de las propiedades de los logaritmos. | |sinopsis=Demostración de las propiedades de los logaritmos. | ||
| }} | }} | ||
| Línea 81: | Línea 81: | ||
| |titulo1=Tutorial 3 | |titulo1=Tutorial 3 | ||
| |duracion=12´43" | |duracion=12´43" | ||
| - | |url1=https://www.youtube.com/watch?v=-6XVI_xzLYw&list=PL3KGq8pH1bFRmhsCe2sPnUj199NNvQWQZ&index=62 | + | |url1=http://www.youtube.com/watch?v=-6XVI_xzLYw&list=PL3KGq8pH1bFRmhsCe2sPnUj199NNvQWQZ&index=62 |
| |sinopsis=Definición del logaritmo de un número. Propiedades. Ejemplos | |sinopsis=Definición del logaritmo de un número. Propiedades. Ejemplos | ||
| }} | }} | ||
| Línea 88: | Línea 88: | ||
| |titulo1=Identidad fundamental del logaritmo | |titulo1=Identidad fundamental del logaritmo | ||
| |duracion=7´58" | |duracion=7´58" | ||
| - | |url1=https://www.youtube.com/watch?v=7tl-EhBIKXo | + | |url1=http://www.youtube.com/watch?v=7tl-EhBIKXo |
| |sinopsis=Identidad fundamental del logaritmo. Ejemplos de aplicación. | |sinopsis=Identidad fundamental del logaritmo. Ejemplos de aplicación. | ||
| }} | }} | ||
| Línea 94: | Línea 94: | ||
| |titulo1=Logaritmo de un producto | |titulo1=Logaritmo de un producto | ||
| |duracion=15'28" | |duracion=15'28" | ||
| - | |url1=https://www.youtube.com/watch?v=_Xb1hOmKUO4 | + | |url1=http://www.youtube.com/watch?v=_Xb1hOmKUO4 |
| |sinopsis=Demostración de la propiedad del logaritmo de un producto. Ejemplos de aplicación. | |sinopsis=Demostración de la propiedad del logaritmo de un producto. Ejemplos de aplicación. | ||
| }} | }} | ||
| Línea 100: | Línea 100: | ||
| |titulo1=Logaritmo de un cociente | |titulo1=Logaritmo de un cociente | ||
| |duracion=12'34" | |duracion=12'34" | ||
| - | |url1=https://www.youtube.com/watch?v=DZLqJGoY_10 | + | |url1=http://www.youtube.com/watch?v=DZLqJGoY_10 |
| |sinopsis=Demostración de la propiedad del logaritmo de un cociente. Ejemplos de aplicación. | |sinopsis=Demostración de la propiedad del logaritmo de un cociente. Ejemplos de aplicación. | ||
| }} | }} | ||
| Línea 106: | Línea 106: | ||
| |titulo1=Logaritmo de una potencia | |titulo1=Logaritmo de una potencia | ||
| |duracion=10'57" | |duracion=10'57" | ||
| - | |url1=https://www.youtube.com/watch?v=oU3Fba5UUEc | + | |url1=http://www.youtube.com/watch?v=oU3Fba5UUEc |
| |sinopsis=Demostración de la propiedad del logaritmo de una potencia. Ejemplos de aplicación. | |sinopsis=Demostración de la propiedad del logaritmo de una potencia. Ejemplos de aplicación. | ||
| }} | }} | ||
| Línea 112: | Línea 112: | ||
| |titulo1=Logaritmo de una raíz | |titulo1=Logaritmo de una raíz | ||
| |duracion=15'24" | |duracion=15'24" | ||
| - | |url1=https://www.youtube.com/watch?v=seWrZZaZHL0 | + | |url1=http://www.youtube.com/watch?v=seWrZZaZHL0 |
| |sinopsis=Demostración de la propiedad del logaritmo de una raíz. Ejemplos de aplicación. | |sinopsis=Demostración de la propiedad del logaritmo de una raíz. Ejemplos de aplicación. | ||
| }} | }} | ||
| Línea 121: | Línea 121: | ||
| |titulo1=Ejercicio 1 | |titulo1=Ejercicio 1 | ||
| |duracion=2´34" | |duracion=2´34" | ||
| - | |url1=https://www.youtube.com/watch?v=3zToR-gkGS0&index=1&list=PLo7_lpX1yruPaD9IzJT-tjN_vFvI1YDjo | + | |url1=http://www.youtube.com/watch?v=3zToR-gkGS0&index=1&list=PLo7_lpX1yruPaD9IzJT-tjN_vFvI1YDjo |
| |sinopsis=Desarrolla: <math>log_4 \, 8^2 \;</math> | |sinopsis=Desarrolla: <math>log_4 \, 8^2 \;</math> | ||
| }} | }} | ||
| Línea 127: | Línea 127: | ||
| |titulo1=Ejercicio 2 | |titulo1=Ejercicio 2 | ||
| |duracion=4´24" | |duracion=4´24" | ||
| - | |url1=https://www.youtube.com/watch?v=u5dm5vQQe_Q&list=PLo7_lpX1yruPaD9IzJT-tjN_vFvI1YDjo&index=2 | + | |url1=http://www.youtube.com/watch?v=u5dm5vQQe_Q&list=PLo7_lpX1yruPaD9IzJT-tjN_vFvI1YDjo&index=2 |
| |sinopsis=Desarrolla: <math>ln \, 5x^3yz^4 \;</math> | |sinopsis=Desarrolla: <math>ln \, 5x^3yz^4 \;</math> | ||
| }} | }} | ||
| Línea 133: | Línea 133: | ||
| |titulo1=Ejercicio 3 | |titulo1=Ejercicio 3 | ||
| |duracion=4´38" | |duracion=4´38" | ||
| - | |url1=https://www.youtube.com/watch?v=2-At_0WIAj8&list=PLo7_lpX1yruPaD9IzJT-tjN_vFvI1YDjo&index=3 | + | |url1=http://www.youtube.com/watch?v=2-At_0WIAj8&list=PLo7_lpX1yruPaD9IzJT-tjN_vFvI1YDjo&index=3 |
| |sinopsis=Desarrolla: <math>ln \, \cfrac{xy^2}{e^3z^4} \;</math> | |sinopsis=Desarrolla: <math>ln \, \cfrac{xy^2}{e^3z^4} \;</math> | ||
| }} | }} | ||
| Línea 139: | Línea 139: | ||
| |titulo1=Ejercicio 4 | |titulo1=Ejercicio 4 | ||
| |duracion=4´47" | |duracion=4´47" | ||
| - | |url1=https://www.youtube.com/watch?v=acI2PRISVNg&list=PLo7_lpX1yruPaD9IzJT-tjN_vFvI1YDjo&index=4 | + | |url1=http://www.youtube.com/watch?v=acI2PRISVNg&list=PLo7_lpX1yruPaD9IzJT-tjN_vFvI1YDjo&index=4 |
| |sinopsis=Desarrolla: <math>log_e \, \sqrt[4]{e^3x^5} \;</math> | |sinopsis=Desarrolla: <math>log_e \, \sqrt[4]{e^3x^5} \;</math> | ||
| }} | }} | ||
| Línea 145: | Línea 145: | ||
| |titulo1=Ejercicio 5 | |titulo1=Ejercicio 5 | ||
| |duracion=3´43" | |duracion=3´43" | ||
| - | |url1=https://www.youtube.com/watch?v=mOROtNjT3DQ&index=5&list=PLo7_lpX1yruPaD9IzJT-tjN_vFvI1YDjo | + | |url1=http://www.youtube.com/watch?v=mOROtNjT3DQ&index=5&list=PLo7_lpX1yruPaD9IzJT-tjN_vFvI1YDjo |
| |sinopsis=Desarrolla: <math>log_3 \, \cfrac{\sqrt[5]{x}}{\sqrt[3]{y}} \;</math> | |sinopsis=Desarrolla: <math>log_3 \, \cfrac{\sqrt[5]{x}}{\sqrt[3]{y}} \;</math> | ||
| }} | }} | ||
| Línea 151: | Línea 151: | ||
| |titulo1=Ejercicio 6 | |titulo1=Ejercicio 6 | ||
| |duracion=5´28" | |duracion=5´28" | ||
| - | |url1=https://www.youtube.com/watch?v=vZfSh92I5F8&list=PLo7_lpX1yruPaD9IzJT-tjN_vFvI1YDjo&index=6 | + | |url1=http://www.youtube.com/watch?v=vZfSh92I5F8&list=PLo7_lpX1yruPaD9IzJT-tjN_vFvI1YDjo&index=6 |
| |sinopsis=Desarrolla: <math>log_5 \, \cfrac{5^x(1-x)}{y^x(x-y^2)} \;</math> | |sinopsis=Desarrolla: <math>log_5 \, \cfrac{5^x(1-x)}{y^x(x-y^2)} \;</math> | ||
| }} | }} | ||
| Línea 161: | Línea 161: | ||
| |titulo1=Ejercicio 1 | |titulo1=Ejercicio 1 | ||
| |duracion=2´07" | |duracion=2´07" | ||
| - | |url1=https://www.youtube.com/watch?v=g68P8Lcssqg&list=PLo7_lpX1yruOQZzFEu7cxWeZffnOaDe4L&index=1 | + | |url1=http://www.youtube.com/watch?v=g68P8Lcssqg&list=PLo7_lpX1yruOQZzFEu7cxWeZffnOaDe4L&index=1 |
| |sinopsis=Expresar como un solo logaritmo: <math>2 log \, x - 3 log \, y</math> | |sinopsis=Expresar como un solo logaritmo: <math>2 log \, x - 3 log \, y</math> | ||
| }} | }} | ||
| Línea 167: | Línea 167: | ||
| |titulo1=Ejercicio 2 | |titulo1=Ejercicio 2 | ||
| |duracion=2´15" | |duracion=2´15" | ||
| - | |url1=https://www.youtube.com/watch?v=90VgizUzIhI&index=2&list=PLo7_lpX1yruOQZzFEu7cxWeZffnOaDe4L | + | |url1=http://www.youtube.com/watch?v=90VgizUzIhI&index=2&list=PLo7_lpX1yruOQZzFEu7cxWeZffnOaDe4L |
| |sinopsis=Expresar como un solo logaritmo: <math>2 ln \, 3 + y ln \, x</math> | |sinopsis=Expresar como un solo logaritmo: <math>2 ln \, 3 + y ln \, x</math> | ||
| }} | }} | ||
| Línea 173: | Línea 173: | ||
| |titulo1=Ejercicio 3 | |titulo1=Ejercicio 3 | ||
| |duracion=2´54" | |duracion=2´54" | ||
| - | |url1=https://www.youtube.com/watch?v=RPRUgbs_K14&index=3&list=PLo7_lpX1yruOQZzFEu7cxWeZffnOaDe4L | + | |url1=http://www.youtube.com/watch?v=RPRUgbs_K14&index=3&list=PLo7_lpX1yruOQZzFEu7cxWeZffnOaDe4L |
| |sinopsis=Expresar como un solo logaritmo: <math>ln \, 4 + 2x</math> | |sinopsis=Expresar como un solo logaritmo: <math>ln \, 4 + 2x</math> | ||
| }} | }} | ||
| Línea 179: | Línea 179: | ||
| |titulo1=Ejercicio 4 | |titulo1=Ejercicio 4 | ||
| |duracion=3´59" | |duracion=3´59" | ||
| - | |url1=https://www.youtube.com/watch?v=KFF_omy3iek&list=PLo7_lpX1yruOQZzFEu7cxWeZffnOaDe4L&index=4 | + | |url1=http://www.youtube.com/watch?v=KFF_omy3iek&list=PLo7_lpX1yruOQZzFEu7cxWeZffnOaDe4L&index=4 |
| |sinopsis=Expresar como un solo logaritmo: <math>2+log_6 \, x - log_6 \, z</math> | |sinopsis=Expresar como un solo logaritmo: <math>2+log_6 \, x - log_6 \, z</math> | ||
| }} | }} | ||
| Línea 185: | Línea 185: | ||
| |titulo1=Ejercicio 5 | |titulo1=Ejercicio 5 | ||
| |duracion=2´30" | |duracion=2´30" | ||
| - | |url1=https://www.youtube.com/watch?v=6lMPBsrGqNs&list=PLo7_lpX1yruOQZzFEu7cxWeZffnOaDe4L&index=5 | + | |url1=http://www.youtube.com/watch?v=6lMPBsrGqNs&list=PLo7_lpX1yruOQZzFEu7cxWeZffnOaDe4L&index=5 |
| |sinopsis=Expresar como un solo logaritmo: <math>log_7 \, x - log_7 \, y - log_7 \, z</math> | |sinopsis=Expresar como un solo logaritmo: <math>log_7 \, x - log_7 \, y - log_7 \, z</math> | ||
| }} | }} | ||
| Línea 194: | Línea 194: | ||
| |titulo1=Ejercicio 1 | |titulo1=Ejercicio 1 | ||
| |duracion=3´19" | |duracion=3´19" | ||
| - | |url1=https://www.youtube.com/watch?v=GXtVPMmmEaE | + | |url1=http://www.youtube.com/watch?v=GXtVPMmmEaE |
| |sinopsis=Si <math>a=ln \, 2</math> y <math>b=ln \, 3</math>, expresa <math>ln \, \cfrac{8}{9}</math> en términos de a y b. | |sinopsis=Si <math>a=ln \, 2</math> y <math>b=ln \, 3</math>, expresa <math>ln \, \cfrac{8}{9}</math> en términos de a y b. | ||
| }} | }} | ||
| Línea 200: | Línea 200: | ||
| |titulo1=Ejercicio 2 | |titulo1=Ejercicio 2 | ||
| |duracion=5´13" | |duracion=5´13" | ||
| - | |url1=https://www.youtube.com/watch?v=gdcMNx1ptME | + | |url1=http://www.youtube.com/watch?v=gdcMNx1ptME |
| |sinopsis=Si <math>ln \, A=5</math>, <math>ln \, B=-2</math> y <math>ln \, C=-7</math>, encuentra el valor numérico de la expresión <math>ln \, \cfrac{A^3 B^4}{C^6}</math>. | |sinopsis=Si <math>ln \, A=5</math>, <math>ln \, B=-2</math> y <math>ln \, C=-7</math>, encuentra el valor numérico de la expresión <math>ln \, \cfrac{A^3 B^4}{C^6}</math>. | ||
| }} | }} | ||
| Línea 206: | Línea 206: | ||
| |titulo1=Ejercicio 3 | |titulo1=Ejercicio 3 | ||
| |duracion=3´23" | |duracion=3´23" | ||
| - | |url1=https://www.youtube.com/watch?v=IpQJT1SMx8U | + | |url1=http://www.youtube.com/watch?v=IpQJT1SMx8U |
| |sinopsis=Escribe como un solo logaritmo: <math>\cfrac{1}{3}\,log\,A+\cfrac{1}{2}\,\left( log\,B - log\,C \right)</math>. | |sinopsis=Escribe como un solo logaritmo: <math>\cfrac{1}{3}\,log\,A+\cfrac{1}{2}\,\left( log\,B - log\,C \right)</math>. | ||
| }} | }} | ||
| Línea 212: | Línea 212: | ||
| |titulo1=Ejercicio 4 | |titulo1=Ejercicio 4 | ||
| |duracion=10´38" | |duracion=10´38" | ||
| - | |url1=https://www.youtube.com/watch?v=mtQRsxiq2Yw&list=PL3KGq8pH1bFRmhsCe2sPnUj199NNvQWQZ&index=63 | + | |url1=http://www.youtube.com/watch?v=mtQRsxiq2Yw&list=PL3KGq8pH1bFRmhsCe2sPnUj199NNvQWQZ&index=63 |
| |sinopsis= | |sinopsis= | ||
| a) Hallar "m" sabiendo que <math>log_m \, 5=2\;</math>. | a) Hallar "m" sabiendo que <math>log_m \, 5=2\;</math>. | ||
| Línea 223: | Línea 223: | ||
| |titulo1=Ejercicio 5 | |titulo1=Ejercicio 5 | ||
| |duracion=15´11" | |duracion=15´11" | ||
| - | |url1=https://www.youtube.com/watch?v=GI1BqXDr2gY&index=64&list=PL3KGq8pH1bFRmhsCe2sPnUj199NNvQWQZ | + | |url1=http://www.youtube.com/watch?v=GI1BqXDr2gY&index=64&list=PL3KGq8pH1bFRmhsCe2sPnUj199NNvQWQZ |
| |sinopsis= | |sinopsis= | ||
| a) Hallar "x" sabiendo que <math>4^{log_x \, 6 \, \cdot \, log_6 \, y \, \cdot \, log_y \, x^4}=x^{log_x \, 4^x}\;</math>. | a) Hallar "x" sabiendo que <math>4^{log_x \, 6 \, \cdot \, log_6 \, y \, \cdot \, log_y \, x^4}=x^{log_x \, 4^x}\;</math>. | ||
| Línea 233: | Línea 233: | ||
| |titulo1=Ejercicio 6 | |titulo1=Ejercicio 6 | ||
| |duracion=13´34" | |duracion=13´34" | ||
| - | |url1=https://www.youtube.com/watch?v=OuT-XxlETMs&list=PL3KGq8pH1bFRmhsCe2sPnUj199NNvQWQZ&index=65 | + | |url1=http://www.youtube.com/watch?v=OuT-XxlETMs&list=PL3KGq8pH1bFRmhsCe2sPnUj199NNvQWQZ&index=65 |
| |sinopsis= | |sinopsis= | ||
| a) Reduce: <math>P=\cfrac{1}{1+log_a \, bc}+ \cfrac{1}{1+log_b \, ac}+\cfrac{1}{1+log_c \, ab}</math>. | a) Reduce: <math>P=\cfrac{1}{1+log_a \, bc}+ \cfrac{1}{1+log_b \, ac}+\cfrac{1}{1+log_c \, ab}</math>. | ||
| Línea 243: | Línea 243: | ||
| |titulo1=Ejercicio 7 | |titulo1=Ejercicio 7 | ||
| |duracion=9´34" | |duracion=9´34" | ||
| - | |url1=https://www.youtube.com/watch?v=p6inEJNKz6Y&index=5&list=PL2287F157D20941E5 | + | |url1=http://www.youtube.com/watch?v=p6inEJNKz6Y&index=5&list=PL2287F157D20941E5 |
| |sinopsis=Desarrolla los siguientes logaritmos: | |sinopsis=Desarrolla los siguientes logaritmos: | ||
| #<math>log \, \cfrac{5z^3u^2}{2x^7}</math> | #<math>log \, \cfrac{5z^3u^2}{2x^7}</math> | ||
| Línea 254: | Línea 254: | ||
| |titulo1=Ejercicios 8 | |titulo1=Ejercicios 8 | ||
| |duracion=8´45" | |duracion=8´45" | ||
| - | |url1=https://www.youtube.com/watch?v=td6Tqzafm_0&index=6&list=PL2287F157D20941E5 | + | |url1=http://www.youtube.com/watch?v=td6Tqzafm_0&index=6&list=PL2287F157D20941E5 |
| |sinopsis=Reduzca las siguientes expresiones a un solo logaritmo: | |sinopsis=Reduzca las siguientes expresiones a un solo logaritmo: | ||
| #<math>2 \, log \, x - 3 \, log \, z</math> | #<math>2 \, log \, x - 3 \, log \, z</math> | ||
| Línea 266: | Línea 266: | ||
| |titulo1=Ejercicio 9 | |titulo1=Ejercicio 9 | ||
| |duracion=7´13" | |duracion=7´13" | ||
| - | |url1=https://www.youtube.com/watch?v=ugfAdqs33A0&index=7&list=PL2287F157D20941E5 | + | |url1=http://www.youtube.com/watch?v=ugfAdqs33A0&index=7&list=PL2287F157D20941E5 |
| |sinopsis=Ejercicios: | |sinopsis=Ejercicios: | ||
| #Expresa <math>log \, \cfrac{0.016^5 \cdot 20}{\sqrt{128}}</math> en función de log 2. | #Expresa <math>log \, \cfrac{0.016^5 \cdot 20}{\sqrt{128}}</math> en función de log 2. | ||
| Línea 274: | Línea 274: | ||
| |titulo1=Ejercicio 10 | |titulo1=Ejercicio 10 | ||
| |duracion=6´18" | |duracion=6´18" | ||
| - | |url1=https://www.youtube.com/watch?v=NE8MA8mSQkU&index=8&list=PL2287F157D20941E5 | + | |url1=http://www.youtube.com/watch?v=NE8MA8mSQkU&index=8&list=PL2287F157D20941E5 |
| |sinopsis=Resuelve: | |sinopsis=Resuelve: | ||
| #Si un número se multiplica por 49, su logaritmo (en base desconocida) aumenta en 2 unidades. Halla la base. | #Si un número se multiplica por 49, su logaritmo (en base desconocida) aumenta en 2 unidades. Halla la base. | ||
| Línea 285: | Línea 285: | ||
| |titulo1=El antilogaritmo | |titulo1=El antilogaritmo | ||
| |duracion=9´31" | |duracion=9´31" | ||
| - | |url1=https://www.youtube.com/watch?v=0UBdJ4MmrSc&t=170s | + | |url1=http://www.youtube.com/watch?v=0UBdJ4MmrSc&t=170s |
| |sinopsis=Definición del antilogaritmo de un número. Ejemplos. | |sinopsis=Definición del antilogaritmo de un número. Ejemplos. | ||
| Línea 293: | Línea 293: | ||
| |titulo1=El cologaritmo | |titulo1=El cologaritmo | ||
| |duracion=10´50" | |duracion=10´50" | ||
| - | |url1=https://www.youtube.com/watch?v=1INfXiu7tTU | + | |url1=http://www.youtube.com/watch?v=1INfXiu7tTU |
| |sinopsis=Definición de cologaritmo de un número. Ejemplos. | |sinopsis=Definición de cologaritmo de un número. Ejemplos. | ||
| Línea 301: | Línea 301: | ||
| |titulo1=Regla de la cadena | |titulo1=Regla de la cadena | ||
| |duracion=16´55" | |duracion=16´55" | ||
| - | |url1=https://www.youtube.com/watch?v=giwItSOXW6E | + | |url1=http://www.youtube.com/watch?v=giwItSOXW6E |
| |sinopsis=Demostración de la regla de la cadena, una generalización de la fórmula del cambio de base: | |sinopsis=Demostración de la regla de la cadena, una generalización de la fórmula del cambio de base: | ||
| Línea 310: | Línea 310: | ||
| |titulo1=Regla del intercambio | |titulo1=Regla del intercambio | ||
| |duracion=11´25" | |duracion=11´25" | ||
| - | |url1=https://www.youtube.com/watch?v=OHuFiaKNvo4 | + | |url1=http://www.youtube.com/watch?v=OHuFiaKNvo4 |
| |sinopsis=Demostración de la regla del intercambio: | |sinopsis=Demostración de la regla del intercambio: | ||
| Línea 320: | Línea 320: | ||
| |titulo1=Ejercicio 1 | |titulo1=Ejercicio 1 | ||
| |duracion=15´24" | |duracion=15´24" | ||
| - | |url1=https://www.youtube.com/watch?v=xaXbIb_x_BM&list=PL3KGq8pH1bFRmhsCe2sPnUj199NNvQWQZ&index=66 | + | |url1=http://www.youtube.com/watch?v=xaXbIb_x_BM&list=PL3KGq8pH1bFRmhsCe2sPnUj199NNvQWQZ&index=66 |
| |sinopsis= | |sinopsis= | ||
| a) Calcula: <math>antilog_2 \, (log_2 \, 8)\;</math>. | a) Calcula: <math>antilog_2 \, (log_2 \, 8)\;</math>. | ||
Revisión actual
Propiedades de los logaritmos:
1: Igualdad y orden:
- a)
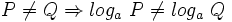 o equivalentemente,
o equivalentemente,
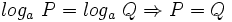
- b)
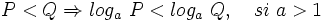
- c)
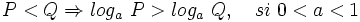
2: Logaritmo de la base:
- a)
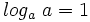
- b)
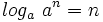
- c)
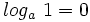
3: Logaritmo de números negativos o nulos:
- Si
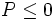 , entonces
, entonces 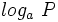 no existe.
no existe.
4: Logaritmo de un producto:
5: Logaritmo de un cociente:
6: Logaritmo de una potencia:
7: Logaritmo de una raíz:
8: Cambio de base:
Tutorial que explica la definición de logaritmo y realiza el cálculo de algunos logaritmos exactos (resultado racional) para comprender el significado de esta operación matemática.
- 00:00 a 03:10: Introducción a logaritmo. Ejercicios de repaso.
- 03:10 a 06:25: Propiedades Básicas.
- 06:25 a 08:30: Propiedad: Logaritmo de un Producto. Demostración.
- 08:30 a 09:20: Propiedad: Logaritmo de una Potencia. Demostración.
- 09:20 a 10:30: Propiedad: Logaritmo de un Cociente. Demostración.
- 10:30 a 13:45: Propiedad: Cambio de Base. Demostración.
- 13:45 a 25:59: Ejercicios de Logaritmos.
Demostración de las propiedades de los logaritmos.
Definición del logaritmo de un número. Propiedades. Ejemplos
Identidad fundamental del logaritmo. Ejemplos de aplicación.
Demostración de la propiedad del logaritmo de un producto. Ejemplos de aplicación.
Demostración de la propiedad del logaritmo de un cociente. Ejemplos de aplicación.
Demostración de la propiedad del logaritmo de una potencia. Ejemplos de aplicación.
Demostración de la propiedad del logaritmo de una raíz. Ejemplos de aplicación.
Desarrollo de logaritmos usando las propiedades:
Desarrolla: 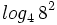
Desarrolla: 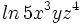
Desarrolla: 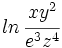
Desarrolla: ![log_e \, \sqrt[4]{e^3x^5} \;](/wikipedia/images/math/9/7/9/979eadabfb3b278c6e762d27ef7878e4.png)
Desarrolla: ![log_3 \, \cfrac{\sqrt[5]{x}}{\sqrt[3]{y}} \;](/wikipedia/images/math/1/6/1/16143fc979664aee83fe3ce7d48fd920.png)
Desarrolla: 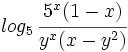
Expresar como un solo logaritmo:
Expresar como un solo logaritmo: 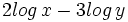
Expresar como un solo logaritmo: 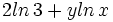
Expresar como un solo logaritmo: 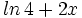
Expresar como un solo logaritmo: 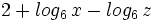
Expresar como un solo logaritmo: 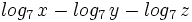
Varios:
Si 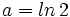 y
y 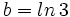 , expresa
, expresa 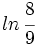 en términos de a y b.
en términos de a y b.
Si 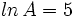 ,
, 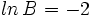 y
y 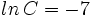 , encuentra el valor numérico de la expresión
, encuentra el valor numérico de la expresión 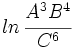 .
.
Escribe como un solo logaritmo: 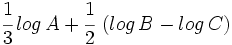 .
.
a) Hallar "m" sabiendo que 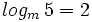 .
.
b) Hallar "x" sabiendo que 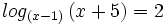 .
.
b) Sabiendo que 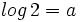 y que
y que 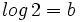 , calcula
, calcula 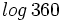 .
.
a) Hallar "x" sabiendo que 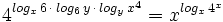 .
.
b) Sabiendo que 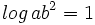 y que
y que 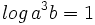 , halla
, halla 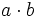 .
.
a) Reduce: 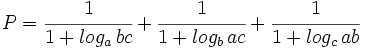 .
.
b) Hallar "x" si 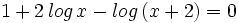 .
.
Desarrolla los siguientes logaritmos:
Reduzca las siguientes expresiones a un solo logaritmo:
Ejercicios:
- Expresa
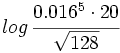 en función de log 2.
en función de log 2.
- Expresa
![log \, \cfrac{12 \sqrt[3]{36}}{\sqrt{0.09^3 \cdot 160}}](/wikipedia/images/math/a/0/3/a03392a26b8add15e65806e0e4e45f6c.png) en función de log 2 y log 3.
en función de log 2 y log 3.
Resuelve:
- Si un número se multiplica por 49, su logaritmo (en base desconocida) aumenta en 2 unidades. Halla la base.
- Resuelve la ecuación
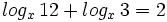
- Determina el menor entero que satisface la condición
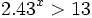
- Determina el mayor real que satisface la condición
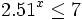
Definición del antilogaritmo de un número. Ejemplos.
Nota: El antilogaritmo es como la inversa del logaritmo, es decir, la exponencial.
Definición de cologaritmo de un número. Ejemplos.
Nota: El cologaritmo es igual al opuesto del logaritmo.
Demostración de la regla de la cadena, una generalización de la fórmula del cambio de base:
Demostración de la regla del intercambio:
a) Calcula:  .
.
b) Halla "x": 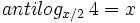 .
.
c) Halla "x": 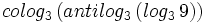 .
.
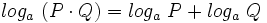
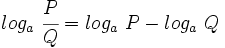
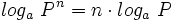
![log_a \ \sqrt[n]{P}=\cfrac{1}{n} \cdot log_a \ P](/wikipedia/images/math/6/c/9/6c919bb3863e8ae2142390b915b8c519.png)
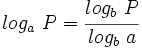
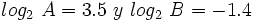 , calcula:
, calcula:
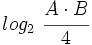
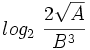
![log_2 \ \cfrac{A \cdot B}{4} \begin{matrix}~_{[5]}~ \\ ~=~ \\ ~ \end{matrix} log_2 \ (A \cdot B) - log_2 \ 4=](/wikipedia/images/math/2/6/d/26d0034bc52ab7b3a2b2d941c430aca1.png)
![\begin{matrix}~_{[4]}~ \\ ~=~ \\ ~ \end{matrix} log_2 \ A + log_2 \ B - log_2 \ 4=3.5-1.4-2=0.1](/wikipedia/images/math/9/7/0/970be2109f6e4e59d97c656098cb0849.png)
![log_2 \ \cfrac{2 \sqrt{A}} {B^3} \begin{matrix}~_{[5]}~ \\ ~=~ \\ ~ \end{matrix} log_2 \ 2 \sqrt{A} - log_2 \ B^3 =](/wikipedia/images/math/0/6/d/06da2c510b8a5216f092a5e9fc5c8b52.png)
![\begin{matrix}~_{[4]}~ \\ ~=~ \\ ~ \end{matrix} log_2 \ 2+ log_2 \sqrt{A} - log_2 \ B^3=1+ log_2 \ A^{\frac{1}{2}} - log_2 B^3=](/wikipedia/images/math/0/f/9/0f9259f963826fa4b14149c91a6d5f6b.png)
![\begin{matrix}~_{[6]}~ \\ ~=~ \\ ~ \end{matrix} 1+ \cfrac{1}{2} ~log_2 \ A - 3 \, log_2 \ B=1+ \cfrac{1}{2} \cdot 3.5 - 3 \cdot (-1.4) = 6.95](/wikipedia/images/math/a/8/4/a84d83f66b2b9058af143a2ae4231ef0.png)
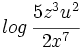
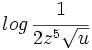
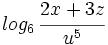
![ln \, \sqrt[3]{\cfrac{x}{z^2u^7}}](/wikipedia/images/math/c/8/5/c851424eddb3c75b5feb58d378224ae7.png)