Plantilla:Circunferencia goniométrica

De Wikipedia

(Diferencia entre revisiones)

Revisión de 18:29 16 oct 2019

Llamaremos circunferencia goniométrica a la circunferencia de radio 1 centrada en un sistema de referencia cartesiano, es decir, con centro en el origen de coordenadas, O.

La circunferencia goniométrica

Tutorial 1 (16´38") Sinopsis:

Definición y propiedades de la circunferencia goniométrica o circunferencia trigonométrica.

Tutorial 2 (7´01") Sinopsis:

Definición y propiedades de la circunferencia goniométrica o circunferencia trigonométrica.

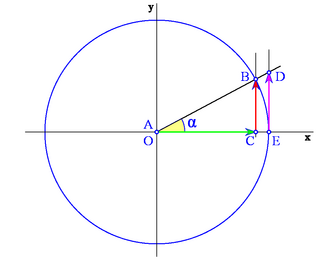
Sobre la circunferencia goniométrica situaremos nuestro ángulo orientado, $\alpha \;$ . Este genera un triángulo rectángulo ABC, tal y como se muestra en la Fig. 2. En él, el vértice A coincide con el origen O, el cateto OC, contiguo al ángulo $\alpha \;$ , se situa en el eje X positivo, y la hipotenusa AB coincide con el radio.

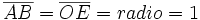
Teniendo en cuenta que $\overline{AB} = \overline{OE}= radio = 1$ , las razones trigonométricas del águlo $\alpha \;$ se expresan de la siguiente manera:

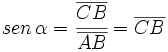
$sen \, \alpha = \cfrac{\overline{CB}}{\overline{AB}}=\overline{CB}$

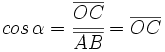
$cos \, \alpha = \cfrac{\overline{OC}}{\overline{AB}}=\overline{OC}$

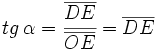
$tg \, \alpha = \cfrac{\overline{DE}}{\overline{OE}}=\overline{DE}$

Fig. 2: Circunferencia goniométrica: De color rojo, el seno; de color verde, el coseno; de color rosa, la tangente

Trigonometría con la circunferencia goniométrica

Tutorial (9´14) Sinopsis:

Empleando un circulo de radio unidad pueden "visualizarse" las razones trigonométricas de un ángulo orientado.

Ejercicio (8´19") Sinopsis:

Dibuja un ángulo $\alpha\;$ en los siguientes casos:

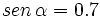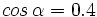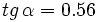
1) $sen\,\alpha=0.7$ 2) $cos\,\alpha=0.4$ 3) $tg\,\alpha=0.56$

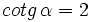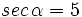4) $cotg\,\alpha=2$ 5) $sec\,\alpha=5$ 3) $cosec\,\alpha=2$

Obtenido de "http://maralboran.org/wikipedia/index.php/Plantilla:Circunferencia_goniom%C3%A9trica"

 }}
 {{p}}
-{{Videotutoriales|titulo=La circunferencia goniométrica
+{{Videotutoriales|titulo=La circunferencia goniométrica|enunciado=
 {{Video_enlace_pildoras
 |titulo1=Tutorial 1

Plantilla:Circunferencia goniométrica

De Wikipedia

Revisión de 18:29 16 oct 2019

Vistas

Herramientas personales

Menú

Buscar

Herramientas