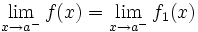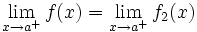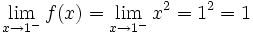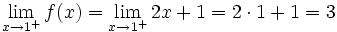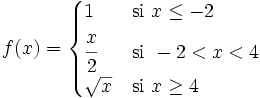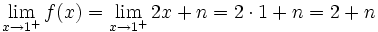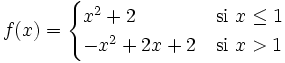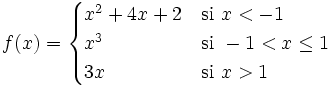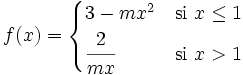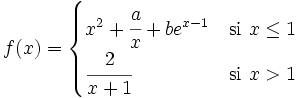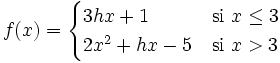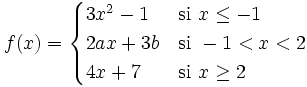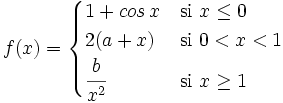Plantilla:Límite de funciones a trozos
De Wikipedia
| Revisión de 18:16 18 mar 2020 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 04:16 1 abr 2020 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 52: | Línea 52: | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Video_enlace | ||
| + | |titulo1=Ejemplo | ||
| + | |duracion=6'57" | ||
| + | |sinopsis=Estudia la continuidad de la función: | ||
| + | |||
| + | :<math>f(x) = \begin{cases} 1 & \mbox{si }x \le -2 \\ \cfrac{x}{2} & \mbox{si } -2<x<4 \\ \sqrt{x} & \mbox{si }x \ge 4 \end{cases}</math> | ||
| + | |||
| + | |url1=https://youtu.be/Q6GraJviAQ4 | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión de 04:16 1 abr 2020
A continuación vamos a ver cómo se estudian los límites de una función definida a trozos. Por simplicidad supondremos que la función consta de sólo dos trozos, pero el procedimiento es extensible a funciones definidas en más de dos trozos.
Procedimiento
Consideremos la siguiente función definida a trozos:
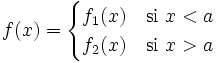
Para el estudio del 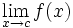 consideraremos los siguientes casos:
consideraremos los siguientes casos:
-
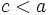 :
: 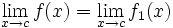
-
 :
: 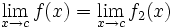
-
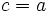 : Es necesario calcular los límites laterales y si éstos coinciden existirá el límite.
: Es necesario calcular los límites laterales y si éstos coinciden existirá el límite.
Ejemplo: Límite de una función definida a trozos
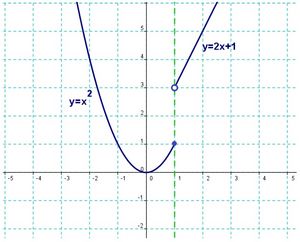
Estudia la continuidad de la siguiente función:
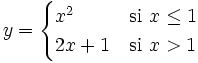
Veamos primero como es la función en cada trozo:
- Si
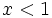 ,
,  es continua por ser una función polinómica, ya que sabemos que toda función polinómica es continua en
es continua por ser una función polinómica, ya que sabemos que toda función polinómica es continua en  , en particular en
, en particular en 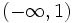 .
.
- Si
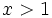 ,
, 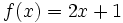 es continua por ser una función polinómica, ya que sabemos que toda función polinómica es continua en
es continua por ser una función polinómica, ya que sabemos que toda función polinómica es continua en  , en particular en
, en particular en 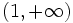 .
.
Falta estudiar la continuidad en 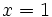 .
.
Recordemos que una función  es continua en
es continua en 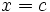 si
si
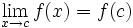
o equivalentemente, si
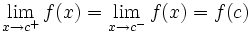
Calculemos los límites laterales y el valor de la función en 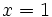 :
:
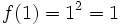 .
.
Como 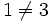 , los límites laterales no coinciden y, por tanto, no existe el límite en
, los límites laterales no coinciden y, por tanto, no existe el límite en 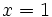 . En consecuencia, la función no es continua en
. En consecuencia, la función no es continua en 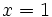 .
.
Estudia la continuidad de la función:
Ejemplo: Límite de una función definida a trozos
Halla el valor del parámetro "n" para que la función sea continua en toda la recta real:
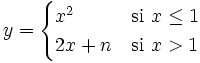
Veamos primero como es la función en cada trozo:
- Si
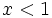 ,
,  es continua por ser una función polinómica, ya que sabemos que toda función polinómica es continua en
es continua por ser una función polinómica, ya que sabemos que toda función polinómica es continua en  , en particular en
, en particular en 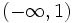 .
.
- Si
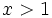 ,
, 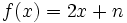 es continua por ser una función polinómica, ya que sabemos que toda función polinómica es continua en
es continua por ser una función polinómica, ya que sabemos que toda función polinómica es continua en  , en particular en
, en particular en 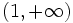 .
.
Falta estudiar la continuidad en 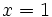 .
.
Recordemos que una función  es continua en
es continua en 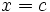 si
si
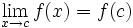
o equivalentemente, si
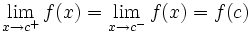
Calculemos los límites laterales y el valor de la función en 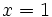 :
:
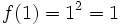 .
.
Para que los dos límites laterales coincidan con 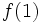 deberá ocurrir que:
deberá ocurrir que:
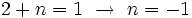
Puedes hacer uso de la siguiente escena de Geogebra para comprobar la solución:
En esta escena podrás representar funciones definidas en hasta 4 trozos.
Estudia la continuidad de la función:
Nota: En este vídeo también estudia la derivabilidad que se verá en el siguiente tema.
Estudia la continuidad de la función:
Nota: En este vídeo también estudia la derivabilidad que se verá en el siguiente tema.
Averigua los valores de "m" para que la siguiente función sea continua en x=1:
Nota: En este vídeo también estudia la derivabilidad que se verá en el siguiente tema.
Averigua los valores de "a" y "b" para que la siguiente función sea continua en x=1:
Nota: En este vídeo también estudia la derivabilidad que se verá en el siguiente tema.
Halla el valor de "h" para que la siguiente función se continua en el conjunto de los números reales:
Halla el valor de "a" y "b" para que la siguiente función se continua en el conjunto de los números reales:
Halla el valor de "a" y "b" para que las siguientes funciones sean continuas en el conjunto de los números reales:
- a)
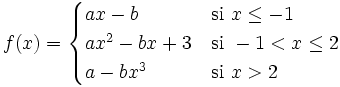
- b)
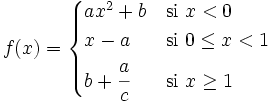
Halla el valor de "a" y "b" para que la siguiente función sea continua en el conjunto de los números reales: