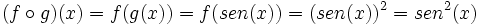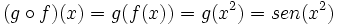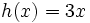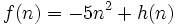Plantilla:Composición de funciones (1ºBach)
De Wikipedia
| Revisión de 09:53 31 mar 2020 Coordinador (Discusión | contribuciones) (→Función compuesta) ← Ir a diferencia anterior |
Revisión de 10:07 31 mar 2020 Coordinador (Discusión | contribuciones) (→Función compuesta) Ir a siguiente diferencia → |
||
| Línea 95: | Línea 95: | ||
| ---- | ---- | ||
| {{Video_enlace_khan | {{Video_enlace_khan | ||
| - | |titulo1=Ejercicio 1 | + | |titulo1=Ejercicio 1a |
| |duracion=2'53" | |duracion=2'53" | ||
| |sinopsis=Halla la composición <math>f \circ g\;</math> y <math>g \circ f\;</math> de las funciones <math>f(x)=\sqrt{x^2-1}\;</math> y <math>g(x)=\cfrac{x}{1+x}\;</math> | |sinopsis=Halla la composición <math>f \circ g\;</math> y <math>g \circ f\;</math> de las funciones <math>f(x)=\sqrt{x^2-1}\;</math> y <math>g(x)=\cfrac{x}{1+x}\;</math> | ||
| Línea 101: | Línea 101: | ||
| }} | }} | ||
| {{Video_enlace_khan | {{Video_enlace_khan | ||
| - | |titulo1=Ejercicio 2 | + | |titulo1=Ejercicio 1b |
| |duracion=6'07" | |duracion=6'07" | ||
| |sinopsis=Halla la composición <math>f \circ g\;</math> y <math>g \circ f\;</math> de las funciones <math>f(x)=x^2+x\;</math> y <math>g(x)=4-x\;</math> | |sinopsis=Halla la composición <math>f \circ g\;</math> y <math>g \circ f\;</math> de las funciones <math>f(x)=x^2+x\;</math> y <math>g(x)=4-x\;</math> | ||
| Línea 107: | Línea 107: | ||
| }} | }} | ||
| {{Video_enlace_khan | {{Video_enlace_khan | ||
| - | |titulo1=Ejercicio 3 | + | |titulo1=Ejercicio 1c |
| |duracion=4'49" | |duracion=4'49" | ||
| |sinopsis=Evaluar funciones compuestas usando tablas | |sinopsis=Evaluar funciones compuestas usando tablas | ||
| Línea 114: | Línea 114: | ||
| }} | }} | ||
| {{Video_enlace_khan | {{Video_enlace_khan | ||
| - | |titulo1=Ejercicio 4 | + | |titulo1=Ejercicio 1d |
| |duracion=3'50" | |duracion=3'50" | ||
| |sinopsis=Dadas las funciones: | |sinopsis=Dadas las funciones: | ||
| Línea 125: | Línea 125: | ||
| }} | }} | ||
| {{Video_enlace_khan | {{Video_enlace_khan | ||
| - | |titulo1=Ejercicio 5 | + | |titulo1=Ejercicio 1e |
| |duracion=3'40" | |duracion=3'40" | ||
| |sinopsis=Evaluar funciones compuestas usando gráficas | |sinopsis=Evaluar funciones compuestas usando gráficas | ||
| |url1=https://www.youtube.com/watch?v=2lilU5xJM0I | |url1=https://www.youtube.com/watch?v=2lilU5xJM0I | ||
| + | }} | ||
| + | {{Video_enlace_matesandres | ||
| + | |titulo1=Ejercicio 2 | ||
| + | |duracion=9'36" | ||
| + | |sinopsis=4 ejercicios sobre composición de funciones | ||
| + | |url1=https://youtu.be/v8j1qoTvDSg | ||
| }} | }} | ||
| {{Video_enlace_fonemato | {{Video_enlace_fonemato | ||
| - | |titulo1=Ejercicio 6 | + | |titulo1=Ejercicio 3a |
| |duracion=16'53" | |duracion=16'53" | ||
| |sinopsis=4 ejercicios sobre composición de funciones | |sinopsis=4 ejercicios sobre composición de funciones | ||
| Línea 137: | Línea 143: | ||
| }} | }} | ||
| {{Video_enlace_fonemato | {{Video_enlace_fonemato | ||
| - | |titulo1=Ejercicio 7 (composición de 3 funciones) | + | |titulo1=Ejercicio 3b (composición de 3 funciones) |
| |duracion=3'50" | |duracion=3'50" | ||
| |sinopsis=Ejercicio sobre la composición de 3 funciones | |sinopsis=Ejercicio sobre la composición de 3 funciones | ||
| Línea 143: | Línea 149: | ||
| }} | }} | ||
| {{Video_enlace_fonemato | {{Video_enlace_fonemato | ||
| - | |titulo1=Ejercicio 8 (composición de 3 funciones) | + | |titulo1=Ejercicio 3c (composición de 3 funciones) |
| |duracion=12'32" | |duracion=12'32" | ||
| |sinopsis=3 ejercicios sobre composición de 3 funciones | |sinopsis=3 ejercicios sobre composición de 3 funciones | ||
Revisión de 10:07 31 mar 2020
Función compuesta
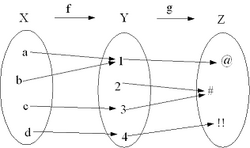
| La función compuesta es una función formada por la aplicación sucesiva de otras dos funciones. Formalmente:
Dadas dos funciones 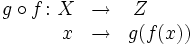 Se aplica sobre el argumento la función más próxima al mismo, y al resultado del cálculo anterior se le aplica finalmente la función restante. 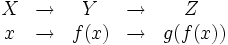 La expresión |
En esta escena analizaremos gráficamente como se obtiene la composición de dos funciones.
Ejemplo: Composición de funciones
Dadas las funciones: 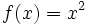 y
y 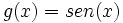
- a) Halla la función
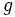 compuesta con
compuesta con  .
.
- b) Halla la función
 compuesta con
compuesta con 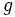 .
.
a) La función 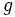 compuesta con
compuesta con  es:
es:
b) La función  compuesta con
compuesta con 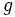 es:
es:
Utiliza la siguiente escena para representar las funciones que acabamos de componer en el ejemplo anterior.
En esta escena podrás ver representadas, de forma conjunta, dos funciones y sus compuestas.
Introducción a la composición de funciones
Introducción a la composición de funciones
Tutorial dedicado a las operaciones con funciones. En este caso la composición de funciones (f o g)(x)
Introducción al concepto de composición o encadenamiento de funciones.
Halla la composición 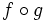 y
y 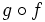 de las funciones
de las funciones 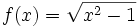 y
y 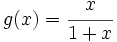
Halla la composición 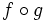 y
y 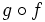 de las funciones
de las funciones 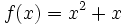 y
y 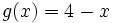
Evaluar funciones compuestas usando tablas
Dadas las funciones:
calcula 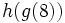 .
.
Evaluar funciones compuestas usando gráficas
4 ejercicios sobre composición de funciones
4 ejercicios sobre composición de funciones
Ejercicio sobre la composición de 3 funciones
3 ejercicios sobre composición de 3 funciones
Este videotutorial te será útil, en especial, para cuando veamos la regla de la cadena en el tema de derivadas.
Este videotutorial te acercará la composición de funciones a modelos prácticos.
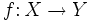 y
y 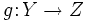 , donde la imagen de
, donde la imagen de 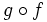 se lee f compuesta con g. Nótese que se nombra, no siguiendo el orden de escritura, sino el orden en que se aplican las funciones a su argumento.
se lee f compuesta con g. Nótese que se nombra, no siguiendo el orden de escritura, sino el orden en que se aplican las funciones a su argumento.