Concepto de función (2º ESO)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 16:22 21 abr 2021 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 16:59 21 abr 2021 Coordinador (Discusión | contribuciones) (→Funciones dadas mediante gráficas) Ir a siguiente diferencia → |
||
| Línea 10: | Línea 10: | ||
| {{Definicion de funcion}} | {{Definicion de funcion}} | ||
| {{p}} | {{p}} | ||
| - | ==Funciones dadas mediante gráficas== | + | ==Formas de expresar una función== |
| - | {{Video_enlace_mas | + | |
| - | |titulo1=Ejemplo | + | |
| - | |duracion=5´44" | + | |
| - | |url1=https://www.youtube.com/watch?v=ei1UAi02egQ | + | |
| - | |sinopsis=Ejercicio en el que debes interpretar una gráfica que relaciona la velocidad de un vehículo con el consumo. | + | |
| - | }} | + | |
Revisión de 16:59 21 abr 2021
Menú:
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Calculadora |
Tabla de contenidos |
Concepto de función
- Una función es una relación entre dos variables (por ejemplo,
 e
e  ) que a cada valor de
) que a cada valor de  le asigna un único valor de
le asigna un único valor de  .
.
- La variable
 se llama variable independiente y la variable
se llama variable independiente y la variable  se llama variable dependiente, porque su valor depende de
se llama variable dependiente, porque su valor depende de  .
.
- Se dice que
 es función de
es función de  y lo representamos por
y lo representamos por 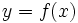 . También se dice que
. También se dice que  es la imagen de
es la imagen de  mediante la función
mediante la función  .
.
"Un grifo vierte agua en un depósito de 200 litros de capacidad, a razón de 2 litros por segundo, hasta que se llena el depósito, momento en el cual se cierra el grifo."
La relación entre el tiempo (t) que el grifo está abierto y el volumen (V) de agua que hay en el depósito es una función.
El volumen es función del tiempo: 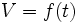
- La variable independiente (t) es el "tiempo que está abierto el grifo".
- La variable dependiente (V) es el "volumen de agua que se ha llenado el depósito".

