Números Reales (PACS)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 08:21 24 sep 2008 Juanmf (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 08:25 24 sep 2008 Juanmf (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 1: | Línea 1: | ||
| - | {{Menú PACS | + | {{Menú Matemáticas 4ESOB |
| - | |ir=[http://maralboran.org/wikipedia/index.php/Dpto._Matem%C3%A1ticas | Indice] | + | |ir= |
| |ampliar= | |ampliar= | ||
| |repasar= | |repasar= | ||
| Línea 6: | Línea 6: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | ==Conjuntos numéricos== | ||
| + | {{Caja_Amarilla|texto=El conjunto formado por los números racionales y los irracionales se llama conjunto de los ''números reales'' y se designa por <math>\mathbb{R}</math>.}} | ||
| + | {{p}} | ||
| + | En el siguiente esquema puedes ver todos los conjuntos númericos con los que hemos trabajado hasta ahora: | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \mbox{Reales } (\mathbb{R}) | ||
| + | \begin{cases} | ||
| + | \mbox{Racionales }(\mathbb{Q}) | ||
| + | \begin{cases} | ||
| + | \mbox{Enteros } (\mathbb{Z}) | ||
| + | \begin{cases} | ||
| + | \mbox{Naturales } (\mathbb{N})\rightarrow 0,1,\frac{16} {2},\sqrt{9}\\ | ||
| + | \mbox{Enteros negativos}\rightarrow -1,\frac{-16} {2},\sqrt{9} | ||
| + | \end{cases}\\ | ||
| + | \mbox{Fraccionarios}\rightarrow 5,23;\frac{5} {2};0,\widehat{54};-\frac{5} {2} | ||
| + | \end{cases}\\ | ||
| + | \mbox{Irracionales } (\mathbb{I})\rightarrow \pi=3.141592654..., e=2.718281..., \varphi = \frac{1 + \sqrt{5}}{2} = 1.618033988... ,\sqrt{2}=1.414213... | ||
| + | \end{cases} | ||
| + | </math> | ||
| + | </center> | ||
| + | {{p}} | ||
| + | |||
| + | ==La recta real== | ||
| + | La '''recta real''' es una representación geométrica del conjunto de los números reales. Tiene su origen en el cero, y se extiende en ambas direcciones, los positivos hacia la derecha y los negativos a la izquierda. Existe una correspondencia uno a uno entre cada punto de la recta y un número real, es decir,''' a cada punto de la recta le corresponde un número real y viceversa'''. | ||
| + | <center> | ||
| + | [[Image:Recta real.png|600px]] | ||
| + | </center> | ||
| + | ''Esta recta numérica real'', se construye como sigue: se elige de manera arbitraria un punto de una línea recta para que represente el cero o punto origen. Se elige un punto a una distancia adecuada a la derecha del origen para que represente al número 1. Esto establece la escala de la recta numérica. | ||
| + | |||
| + | ==Representación de números sobre la recta real== | ||
| + | Todo número real puede situarse sobre la recta real, dependiendo de cómo sea el número: | ||
| + | |||
| + | ===Entero o decimal exacto=== | ||
| + | Vamos intentar representar un número al azar, el 3,24 por ejemplo, buscamos el 3,2 primero, "ampliamos" buscamos el 3,24 y marcamos. | ||
| + | |||
| + | [[Imagen:Recta real entero o decimal exacto.png|center]] | ||
| + | ===Decimal periódico=== | ||
| + | {| | ||
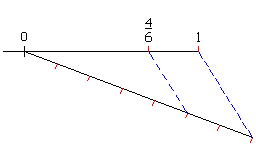
| + | |Hacemos con la regla una recta oblicua a la primera y que mida un múltiplo del denominador dividimos esta nueva recta en tantas partes como indique el denominador (si el denominador es 7 dividimos en siete partes), unimos sus extremos y trazamos las paralelas.|| [[Imagen:Recta real decimal periodico.png]] | ||
| + | |} | ||
| + | ===Radical cuadrático=== | ||
| + | {| | ||
| + | |Podemos representar un radical cuadrático teniendo en cuenta el teorema de Pitágoras. En el ejemplo, se muestra como se ha representado <math>\sqrt{13}</math>|| [[Imagen:Recta real radical cuadratico.png]] | ||
| + | |} | ||
| + | ===Resto de irracionales=== | ||
| + | En este caso se toma su expresión aproximada decimal y se afina tanto como se quiera empleando el método mostrado en decimales exactos. | ||
| + | |||
| + | |||
| + | [[Categoría: Matemáticas|Números]][[Categoría: Números|Reales]] | ||
Revisión de 08:25 24 sep 2008
Menú:
| Enlaces internos | Para repasar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Calculadora |
Tabla de contenidos |
Conjuntos numéricos
El conjunto formado por los números racionales y los irracionales se llama conjunto de los números reales y se designa por 
.
En el siguiente esquema puedes ver todos los conjuntos númericos con los que hemos trabajado hasta ahora:
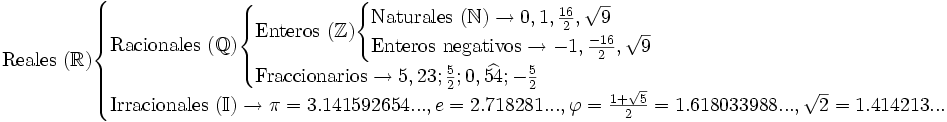
La recta real
La recta real es una representación geométrica del conjunto de los números reales. Tiene su origen en el cero, y se extiende en ambas direcciones, los positivos hacia la derecha y los negativos a la izquierda. Existe una correspondencia uno a uno entre cada punto de la recta y un número real, es decir, a cada punto de la recta le corresponde un número real y viceversa.
Representación de números sobre la recta real
Todo número real puede situarse sobre la recta real, dependiendo de cómo sea el número:
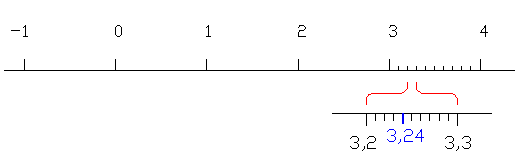
Entero o decimal exacto
Vamos intentar representar un número al azar, el 3,24 por ejemplo, buscamos el 3,2 primero, "ampliamos" buscamos el 3,24 y marcamos.
Decimal periódico
| Hacemos con la regla una recta oblicua a la primera y que mida un múltiplo del denominador dividimos esta nueva recta en tantas partes como indique el denominador (si el denominador es 7 dividimos en siete partes), unimos sus extremos y trazamos las paralelas. | 
|
Radical cuadrático
Podemos representar un radical cuadrático teniendo en cuenta el teorema de Pitágoras. En el ejemplo, se muestra como se ha representado  |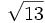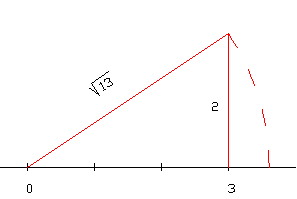 
|
Resto de irracionales
En este caso se toma su expresión aproximada decimal y se afina tanto como se quiera empleando el método mostrado en decimales exactos.
