Pappus
De Wikipedia
| Revisión de 00:55 2 ene 2009 Coordinador (Discusión | contribuciones) (→Cadena de Pappus) ← Ir a diferencia anterior |
Revisión de 00:56 2 ene 2009 Coordinador (Discusión | contribuciones) (→Cadena de Pappus) Ir a siguiente diferencia → |
||
| Línea 54: | Línea 54: | ||
| [[Imagen:cadenapappus.png|thumb|left|Cadena de Pappus]] | [[Imagen:cadenapappus.png|thumb|left|Cadena de Pappus]] | ||
| La figura sombreada formada por estos círcuos tangentes, se denomina ''Cadena de Pappus'' y se debe a Pappus. | La figura sombreada formada por estos círcuos tangentes, se denomina ''Cadena de Pappus'' y se debe a Pappus. | ||
| + | |||
| + | para más información ver: [http://en.wikipedia.org/wiki/Pappus_chain] | ||
| [[Categoría: Matemáticas]][[Categoría: Historia de las Matemáticas]][[Categoría: Matemáticos]] | [[Categoría: Matemáticas]][[Categoría: Historia de las Matemáticas]][[Categoría: Matemáticos]] | ||
Revisión de 00:56 2 ene 2009
Pappus de Alejandría (c. 290 – c. 350), matemático griego.
Último gran matemático de la escuela alejandrina, escribió comentarios a los Elementos de Euclides y al Almagesto de Ptolomeo.
El siglo IV es, en general, un período de estancamiento en los estudios matemáticos, en el que Pappus se destaca como una notable excepción. Qué lejos estaba por encima de sus contemporáneos, que poco apreciado o entendido por ellos, como se demuestra por la ausencia de referencias a él en otros escritores griegos, y por el hecho de que su obra no tuvo ningún efecto en detener la decadencia de la ciencia matemática. A este respecto, la suerte de Pappus fue sorprendentemente similar a la de Diophantus.
Su obra principal, Synagoge o Colección matemática, escrita hacia el 340, reviste una particular importancia desde el punto de vista histórico porque, además de ser una exposición completa y sistemática de los conocimientos matemáticos de su época, recoge fragmentos, a veces íntegros, de las obras que constituían los fundamentos de la enseñanza de las matemáticas en la ciudad de Alejandría, hoy en gran parte perdidas. La Colección, compuesta por ocho libros, casi todos conservados (excepto el primero y parte del segundo), contiene una serie de problemas que introducen nociones geométricas importantes, como el foco de una parábola o la directriz de una cónica, y los enunciados de muchos teoremas, entre ellos, el que expresa la superficie y el volumen de las figuras de revolución.
Tabla de contenidos |
Geometría
En geometría, se le atribuyen varios teoremas. Entre éstos están:
Teorema del centroide de Pappus
El teorema del centroide de Pappus, también conocido como teorema de Guldin, teorema de Pappus-Guldin o teorema de Pappus, es el nombre de dos teoremas que relacionan superficies y volúmenes de sólidos de revolución.
Los teoremas se les atribuyen a Pappus y a Paul Guldin.
Primer Teorema de Pappus
El área, A de una superficie de revolución generada mediante la rotación de una curva plana C alrededor de un eje externo a C sobre el mismo plano, es igual a la longitud de C, s, multiplicada por la distancia, d, recorrida por su centroide en una rotación completa alrededor de dicho eje.

Por ejemplo, el área de la superficie de un toro de radio menor r y radio mayor R es
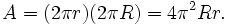
Segundo Teorema de Pappus
El volumen, V, de un sólido de revolución generado mediante la rotación de un área plana alrededor de un eje externo, es igual al producto del área, A, por la distancia, d recorrida por su centroide en una rotación completa alrededor del eje.
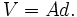
Por ejemplo, el volumen de un toro de radio menor r y radio mayor R es
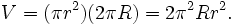
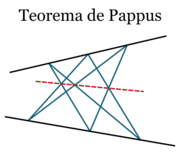
Teorema del hexágono de Pappus
Teorema del hexágono de Pappus
Si en un par de rectas escogemos tres puntos al azar en cada una y los unimos dos a dos, las intersecciones de las rectas que los unen estarán en una línea recta.
Puede considerarse como un caso particular del Teorema de Pascal (que afirma lo mismo para cualquier cónica).
Es un teorema puramente de incidencia (no hace referencia a medidas) pero se demuestra usando los axiomas de congruencia de segmentos. Es importante en el sistema axiomático de la Geometría Proyectiva, ya que introducido como axioma permite demostrar todos los teoremas de incidencia conocidos sin tener que introducir axiomas métricos. Gracias a esto, podemos considerar la geometría proyectiva como una geometría puramente de incidencia.
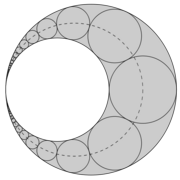
Cadena de Pappus
La figura sombreada formada por estos círcuos tangentes, se denomina Cadena de Pappus y se debe a Pappus.
para más información ver: [1]