Radicales (1ºBach)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 18:13 9 ene 2009 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 18:24 9 ene 2009 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 6: | Línea 6: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | ==Raíces=={{Caja_Amarilla|texto= | + | ==Raíces== |
| + | {{Caja_Amarilla|texto= | ||
| Sdefine '''raíz n-sima''' de un número real <math>a\;\!</math> (y se representa por <math>\sqrt[n]{a}</math>) como otro número real <math>b\;\!</math> tal que <math>b^n =a\;\!</math>. <math>(n \in \mathbb{N},\ n>1)</math> | Sdefine '''raíz n-sima''' de un número real <math>a\;\!</math> (y se representa por <math>\sqrt[n]{a}</math>) como otro número real <math>b\;\!</math> tal que <math>b^n =a\;\!</math>. <math>(n \in \mathbb{N},\ n>1)</math> | ||
| Línea 16: | Línea 17: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | ===La raíz como potencia de exponente fraccionario=== | ||
| + | {{Teorema| | ||
| + | titulo=Proposición | ||
| + | |enunciado= | ||
| + | *Toda raíz se puede expresar como una potencia cuya base es el radicando, <math>a\;\!</math>, y el exponente es <math>\cfrac{1}{n}</math>, siendo <math>n\;\!</math> el índice de la raíz. Ésto es:{{p}} | ||
| + | {{Caja|contenido=<math>\sqrt[n]{a}=a^\frac{1}{n}</math>}} | ||
| + | *De forma similar, también se cumple:{{p}} | ||
| + | {{Caja|contenido=<math>\sqrt[n]{a^m}=a^\frac{m}{n}</math>}} | ||
| + | |demo= | ||
| + | Para la primera parte, basta con ver que se cumple la condición de la definición de raíz. | ||
| + | |||
| + | <center><math>(a^\frac{1}{n})^n=a^{\frac{1}{n} \cdot n}=a^1=a</math></center> | ||
| + | |||
| + | Para la segunda parte, haremos una comprobación análoga: | ||
| + | |||
| + | <center><math>(a^\frac{m}{n})^n=a^{\frac{m}{n} \cdot n}=a^m</math></center> | ||
| + | |||
| + | }} | ||
| + | {{Desplegable|titulo=Ejemplos:{{b}}|contenido= | ||
| + | {{p}} | ||
| + | Pulsa el botón "Ejemplo" para ver distintos ejemplos y anótalos en tu cuaderno: | ||
| + | |||
| + | <center><iframe> | ||
| + | url=http://maralboran.org/web_ma/descartes/3_eso/Radicales/radicales1_2.html | ||
| + | width=500 | ||
| + | height=230 | ||
| + | name=myframe | ||
| + | </iframe></center> | ||
| + | |||
| + | <center>[http://maralboran.org/web_ma/descartes/3_eso/Radicales/radicales1_2.html '''Click''' aquí si no se ve bien la escena]</center> | ||
| + | |||
| + | }} | ||
| + | {{p}} | ||
| + | {{Ejemplo|titulo=Ejemplo: La raíz como potencia de exponente fraccionario'' | ||
| + | |enunciado= | ||
| + | ::Escribe las siguientes potencias de exponente fraccionario en forma de raíces y calcula su valor: | ||
| + | ::<math>a)\ 16^\frac{3}{4}\quad b)\ 27^\frac{2}{3}\quad c)\ 125^\frac{4}{3}\quad d)\ 100^{-\frac{3}{2}}\quad e)\ 8^{-\frac{2}{3}}</math> | ||
| + | |sol= | ||
| + | Utiliza la siguiente escena para comprobar su resultado. Aumenta el número de decimales cuando sea necesario. | ||
| + | {{p}} | ||
| + | <center><iframe> | ||
| + | url=http://maralboran.org/web_ma/descartes/3_eso/Potencias/potencias33_2.html | ||
| + | width=570 | ||
| + | height=240 | ||
| + | name=myframe | ||
| + | </iframe></center> | ||
| + | <center>[http://maralboran.org/web_ma/descartes/3_eso/Potencias/potencias33_2.html '''Click''' aquí si no se ve bien la escena]</center> | ||
| + | }} | ||
| + | {{p}} | ||
| + | |||
| + | [[Categoría: Matemáticas]][[Categoría: Números]] | ||
Revisión de 18:24 9 ene 2009
Menú:
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Raíces
Sdefine raíz n-sima de un número real  (y se representa por
(y se representa por ![\sqrt[n]{a}](/wikipedia/images/math/9/a/2/9a2b6d33f3d62a1e8bd99c76f3cb79f5.png) ) como otro número real
) como otro número real  tal que
tal que 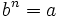 .
. 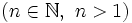
Es decir:
![b=\sqrt[n]{a} \iff b^n =a](/wikipedia/images/math/a/8/5/a854f42279a8ade5b0082bc477d30b79.png)
El número  se llama radicando, el número
se llama radicando, el número  , índice y
, índice y  es la raíz.
es la raíz.
La raíz como potencia de exponente fraccionario
Proposición
- Toda raíz se puede expresar como una potencia cuya base es el radicando,
 , y el exponente es
, y el exponente es 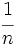 , siendo
, siendo  el índice de la raíz. Ésto es:
el índice de la raíz. Ésto es:
|
|
- De forma similar, también se cumple:
|
|
Demostración:
Para la primera parte, basta con ver que se cumple la condición de la definición de raíz.
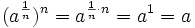
Para la segunda parte, haremos una comprobación análoga:
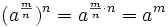
Ejemplos:
Pulsa el botón "Ejemplo" para ver distintos ejemplos y anótalos en tu cuaderno:
Ejemplo: La raíz como potencia de exponente fraccionario
- Escribe las siguientes potencias de exponente fraccionario en forma de raíces y calcula su valor:
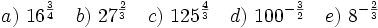
Solución:
Utiliza la siguiente escena para comprobar su resultado. Aumenta el número de decimales cuando sea necesario.
![\sqrt[n]{a}=a^\frac{1}{n}](/wikipedia/images/math/2/0/0/2009af813099ac7b1bef0f0fb92a7999.png)
![\sqrt[n]{a^m}=a^\frac{m}{n}](/wikipedia/images/math/3/b/0/3b0234682d54453ceee722e89c782c2e.png)

