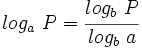Logaritmos (1ºBach)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 09:22 10 ene 2009 Coordinador (Discusión | contribuciones) (→Propiedades de los logaritmos) ← Ir a diferencia anterior |
Revisión de 09:23 10 ene 2009 Coordinador (Discusión | contribuciones) (→Propiedades de los logaritmos) Ir a siguiente diferencia → |
||
| Línea 26: | Línea 26: | ||
| {{Caja_Amarilla|texto= | {{Caja_Amarilla|texto= | ||
| '''1: Igualdad y orden:''' | '''1: Igualdad y orden:''' | ||
| - | :a) <math>P \ne Q \Rightarrow log_a \ P \ne log_a \ Q</math>. | + | :a) <math>P \ne Q \Rightarrow log_a \ P \ne log_a \ Q</math> |
| - | :b) <math>P < Q \Rightarrow log_a \ P < log_a \ Q, \quad \forall a>1</math>. | + | :b) <math>P < Q \Rightarrow log_a \ P < log_a \ Q, \quad \forall a>1</math> |
| '''2: Logaritmo de la base:''' | '''2: Logaritmo de la base:''' | ||
| - | : <math>log_a \ a=1</math>. | + | : <math>log_a \ a=1</math> |
| '''3: Logaritmo de 1:''' | '''3: Logaritmo de 1:''' | ||
| - | : <math>log_a \ 1=0</math>. | + | : <math>log_a \ 1=0</math> |
| '''4: Logaritmo de un producto:''' | '''4: Logaritmo de un producto:''' | ||
| - | : <math>log_a \ (P \cdot Q)=log_a \ P + log_a \ Q</math>. | + | : <math>log_a \ (P \cdot Q)=log_a \ P + log_a \ Q</math> |
| '''5: Logaritmo de un cociente:''' | '''5: Logaritmo de un cociente:''' | ||
| - | : <math>log_a \ \cfrac{P}{Q}=log_a \ P - log_a \ Q</math>. | + | : <math>log_a \ \cfrac{P}{Q}=log_a \ P - log_a \ Q</math> |
| '''6: Logaritmo de una potencia:''' | '''6: Logaritmo de una potencia:''' | ||
| - | : <math>log_a \ P^n=n \cdot log_a \ P</math>. | + | : <math>log_a \ P^n=n \cdot log_a \ P</math> |
| '''7: Logaritmo de una raíz:''' | '''7: Logaritmo de una raíz:''' | ||
| - | : <math>log_a \ \sqrt{n}{P}=\cfrac{1}{n} \cdot log_a \ P</math>. | + | : <math>log_a \ \sqrt[n]{P}=\cfrac{1}{n} \cdot log_a \ P</math> |
| '''8: Cambio de base:''' | '''8: Cambio de base:''' | ||
| - | : <math>log_a \ P=\cfrac{log_b \ P}{log_b \ a}</math>. | + | : <math>log_a \ P=\cfrac{log_b \ P}{log_b \ a}</math> |
| }} | }} | ||
Revisión de 09:23 10 ene 2009
Menú:
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
Logaritmos
Dado un número real 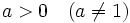 , se define el logaritmo en base a de un número real
, se define el logaritmo en base a de un número real 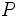 , y se designa
, y se designa 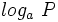 , al exponente
, al exponente  al que hay que elevar la base
al que hay que elevar la base  para obtener
para obtener 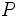 , es decir:
, es decir:
|
|
Por consiguiente, podemos ver al logaritmo como la operación inversa de la potenciación.
Propiedades de los logaritmos
1: Igualdad y orden:
- a)
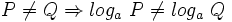
- b)
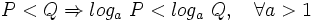
2: Logaritmo de la base:
3: Logaritmo de 1:
4: Logaritmo de un producto:
5: Logaritmo de un cociente:
6: Logaritmo de una potencia:
7: Logaritmo de una raíz:
8: Cambio de base:
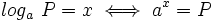
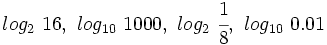
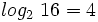 porque
porque 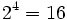
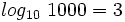 porque
porque 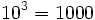
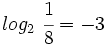 porque
porque 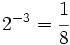
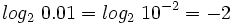 porque
porque 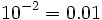
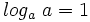
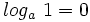
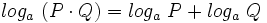
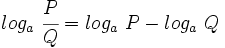
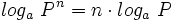
![log_a \ \sqrt[n]{P}=\cfrac{1}{n} \cdot log_a \ P](/wikipedia/images/math/6/c/9/6c919bb3863e8ae2142390b915b8c519.png)