Logaritmos (1ºBach)
De Wikipedia
| Revisión de 09:23 10 ene 2009 Coordinador (Discusión | contribuciones) (→Propiedades de los logaritmos) ← Ir a diferencia anterior |
Revisión de 09:32 10 ene 2009 Coordinador (Discusión | contribuciones) (→Logaritmos decimales) Ir a siguiente diferencia → |
||
| Línea 45: | Línea 45: | ||
| ==Logaritmos decimales== | ==Logaritmos decimales== | ||
| + | {{Caja_Amarilla|texto= | ||
| + | Los '''logaritmos decimales''' son aquellos cuya base es 10. En vez de representarlos por <math>log_{10}\;</math>, los representaremos, simplemente, por <math>log\;</math>. Esto es: | ||
| + | <center><math>log_{10} \ P=log \ P</math></center> | ||
| + | }} | ||
| + | {{p}} | ||
| + | Haciendo uso de la propiedad del cambio de base, vista en el apartado anterior, podemos calcular logaritmos en cualquier base utilizando logaritmos decimales. | ||
| + | Antes de la existencia de las calculadoras, los logaritmos decimales se obtenían a partir de unas '''tablas logarítmicas''' | ||
| + | |||
| ==Logaritmos neperianos== | ==Logaritmos neperianos== | ||
| [[Categoría: Matemáticas]][[Categoría: Números]] | [[Categoría: Matemáticas]][[Categoría: Números]] | ||
Revisión de 09:32 10 ene 2009
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
Logaritmos
Dado un número real 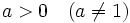 , se define el logaritmo en base a de un número real
, se define el logaritmo en base a de un número real 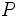 , y se designa
, y se designa 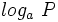 , al exponente
, al exponente  al que hay que elevar la base
al que hay que elevar la base  para obtener
para obtener 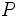 , es decir:
, es decir:
|
|
Por consiguiente, podemos ver al logaritmo como la operación inversa de la potenciación.
Propiedades de los logaritmos
1: Igualdad y orden:
- a)
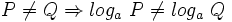
- b)
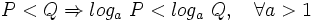
2: Logaritmo de la base:
3: Logaritmo de 1:
4: Logaritmo de un producto:
5: Logaritmo de un cociente:
6: Logaritmo de una potencia:
7: Logaritmo de una raíz:
8: Cambio de base:
Logaritmos decimales
Los logaritmos decimales son aquellos cuya base es 10. En vez de representarlos por 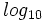 , los representaremos, simplemente, por
, los representaremos, simplemente, por 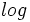 . Esto es:
. Esto es:
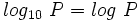
Haciendo uso de la propiedad del cambio de base, vista en el apartado anterior, podemos calcular logaritmos en cualquier base utilizando logaritmos decimales. Antes de la existencia de las calculadoras, los logaritmos decimales se obtenían a partir de unas tablas logarítmicas
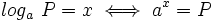
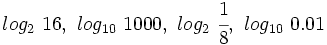
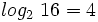 porque
porque 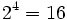
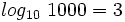 porque
porque 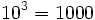
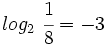 porque
porque 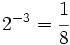
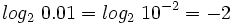 porque
porque 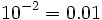
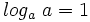
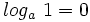
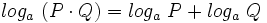
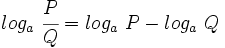
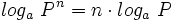
![log_a \ \sqrt[n]{P}=\cfrac{1}{n} \cdot log_a \ P](/wikipedia/images/math/6/c/9/6c919bb3863e8ae2142390b915b8c519.png)