Estudio gráfico (PACS)
De Wikipedia
| Revisión de 09:35 15 ene 2009 Coordinador (Discusión | contribuciones) (→Monotonía) ← Ir a diferencia anterior |
Revisión de 09:39 15 ene 2009 Coordinador (Discusión | contribuciones) (→Extremos relativos: Máximos y mínimos) Ir a siguiente diferencia → |
||
| Línea 12: | Línea 12: | ||
| ==Extremos relativos: Máximos y mínimos== | ==Extremos relativos: Máximos y mínimos== | ||
| - | {{Caja Amarilla | + | {{Máximos y mínimos de una función}} |
| - | |texto= | + | {{p}} |
| - | Una función <math>y = f(x)</math> tiene un '''máximo''' en un punto <math>(x_o,y_o)</math> cuando <math>y_o</math> es mayor que los valores que toma la variable <math>y</math> en un intervalo entorno al punto. | + | |
| - | Una función <math>y = f(x)</math> tiene un '''mínimo''' en un punto <math>(x_o,y_o)</math> cuando <math>y_o</math> es menor que los valores que toma la variable <math>y</math> en un intervalo entorno al punto. | + | |
| - | }}{{p}} | + | |
| - | {{AI2|titulo=Actividad interactiva: ''Crecimiento, máximos y mínimos'' | + | |
| - | |cuerpo= | + | |
| - | {{ai_cuerpo | + | |
| - | |enunciado= | + | |
| - | 1. Interpreta la siguiente gráfica que muestra las temperaturas a lo largo de un día de invierno en un pueblo de Valladolid. | + | |
| - | |actividad= | + | |
| - | La siguiente gráfica muestra las temperaturas a lo largo de un día de invierno en un pueblo de Valladolid. En el eje horizontal hemos representado las horas del día y en el eje vertical, las temperaturas. | + | |
| - | + | ||
| - | Cuando éstas aumentan decimos que la función es creciente. Cuando disminuyen, diremos que es decreciente. | + | |
| - | + | ||
| - | En aquellos puntos de la gráfica de una función donde pasa de ser decreciente a ser creciente decimos que alcanza un mínimo. En los puntos que pasa de ser creciente a ser decreciente alcanza un máximo. | + | |
| - | + | ||
| - | <center><iframe> | + | |
| - | url=http://maralboran.ath.cx/web_ma/descartes/1y2_eso/Interpretacion_de_graficas/Graficas_4.html | + | |
| - | width=560 | + | |
| - | height=400 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | + | ||
| - | Haz click con el ratón en los puntos de la gráfica de los que quieras saber sus coordenadas y contesta: | + | |
| - | + | ||
| - | a) ¿Qué temperatura hizo a las 0 horas? ¿Y a las 10 horas? | + | |
| - | + | ||
| - | b) ¿A qué hora había 0º? | + | |
| - | + | ||
| - | c) ¿A qué hora se alcanzó la temperatura máxima del día?¿Cuál fue la temperatura máxima? | + | |
| - | + | ||
| - | d) ¿A qué hora se alcanzo la temperatura mínima del día? ¿Cuál fue la temperatura mínima? | + | |
| - | + | ||
| - | e) ¿En que periodo del día subió la temperatura? ¿En qué periodo bajó? ¿En qué periodos se mantuvo constante? | + | |
| - | + | ||
| - | f) ¿En qué período del día hubo una temperatura por debajo de 0º? | + | |
| - | + | ||
| - | g) Construye una tabla con las temperaturas que se registraron a lo largo del día. | + | |
| - | + | ||
| - | <table border="1" width="100%"> | + | |
| - | <tr> | + | |
| - | <td width="8%"><strong>Hora</strong></td> | + | |
| - | <td align="center" width="6%"><strong>0</strong></td> | + | |
| - | <td align="center" width="6%"><strong>2</strong></td> | + | |
| - | <td align="center" width="6%"><strong>4</strong></td> | + | |
| - | <td align="center" width="6%"><strong>6</strong></td> | + | |
| - | <td align="center" width="6%"><strong>8</strong></td> | + | |
| - | <td align="center" width="6%"><strong>10</strong></td> | + | |
| - | <td align="center" width="6%"><strong>12</strong></td> | + | |
| - | <td align="center" width="6%"><strong>14</strong></td> | + | |
| - | <td align="center" width="6%"><strong>16</strong></td> | + | |
| - | <td align="center" width="7%"><strong>18</strong></td> | + | |
| - | <td align="center" width="7%"><strong>20</strong></td> | + | |
| - | <td align="center" width="7%"><strong>22</strong></td> | + | |
| - | <td align="center" width="7%"><strong>24</strong></td> | + | |
| - | </tr> | + | |
| - | <tr> | + | |
| - | <td width="8%"><strong>Temperatura</strong></td> | + | |
| - | <td width="6%"> </td> | + | |
| - | <td width="6%"> </td> | + | |
| - | <td width="6%"> </td> | + | |
| - | <td width="6%"> </td> | + | |
| - | <td width="6%"> </td> | + | |
| - | <td width="6%"> </td> | + | |
| - | <td width="6%"> </td> | + | |
| - | <td width="6%"> </td> | + | |
| - | <td width="6%"> </td> | + | |
| - | <td width="7%"> </td> | + | |
| - | <td width="7%"> </td> | + | |
| - | <td width="7%"> </td> | + | |
| - | <td width="7%"> </td> | + | |
| - | </tr> | + | |
| - | </table> | + | |
| - | }} | + | |
| - | {{ai_cuerpo | + | |
| - | |enunciado=2. Construye una grafica que cumpla ciertas condiciones de crecimiento, de máximos y mínimos. | + | |
| - | |actividad= | + | |
| - | En la siguiente escena se representa la gráfica de una función creciente en el intervalo [0,8], decreciente en el intervalo [8,16] y creciente de nuevo en el intervalo [16,24]. La función alcanza un máximo en el punto B y un mínimo en el punto C. | + | |
| - | + | ||
| - | <center><iframe> | + | |
| - | url=http://maralboran.ath.cx/web_ma/descartes/1y2_eso/Interpretacion_de_graficas/Graficas_5.html | + | |
| - | width=560 | + | |
| - | height=400 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | + | ||
| - | Arrastra los puntos A, B, C y D para representar gráficas con las siguientes características. En cada caso, escribe en tu cuaderno en qué intervalos la función es creciente y en cuáles es decreciente: | + | |
| - | + | ||
| - | a) Pasa por los puntos (0,3) y (24,0), alcanza un máximo en el punto (8,6), un mínimo en el punto (16,-5). | + | |
| - | + | ||
| - | b) Pasa por el punto (0,5) y se mantiene constante en todo el intervalo [0, 8], alcanza un mínimo en (16, -1) y un máximo en (24,8). | + | |
| - | }} | + | |
| - | {{ai_cuerpo | + | |
| - | |enunciado=3. Autoevaluación. | + | |
| - | |actividad= | + | |
| - | <center><iframe> | + | |
| - | url=http://contenidos.santillanaenred.com/jukebox/servlet/GetPlayerP3V?p3v=true&xref=200412031131_AC_0_1931782083&mode=1&rtc=1001&locale=es&cache=false',750,540,'snrPop',0 | + | |
| - | width=100% | + | |
| - | height=700 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | }} | + | |
| - | }} | + | |
| ===Ejercicios=== | ===Ejercicios=== | ||
| {{ejercicio | {{ejercicio | ||
| Línea 130: | Línea 28: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | |||
| ==Tendencias== | ==Tendencias== | ||
| {{Tendencias de una función}} | {{Tendencias de una función}} | ||
Revisión de 09:39 15 ene 2009
| Enlaces internos | Para repasar | Enlaces externos |
| Indice CD Alumno 07 Resueltos 07 Descartes Manual Casio | Coordenadas Funciones (SM) Funciones (ppt) Descartes: Test de ejercicios | WIRIS Calculadora |
Tabla de contenidos |
Monotonía
- Una función es creciente en un intervalo I cuando al aumentar la variable independiente
 en ese intervalo, aumenta la variable dependiente
en ese intervalo, aumenta la variable dependiente  .
.
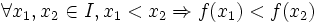
- Una función es decreciente en un intervalo cuando al aumentar la variable independiente
 en ese intervalo, disminuye la variable dependiente
en ese intervalo, disminuye la variable dependiente  .
.
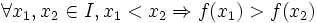
- Una función es constante en un intervalo cuando al aumentar la variable independiente
 en ese intervalo, la variable dependiente
en ese intervalo, la variable dependiente  no varía, siempre toma un mismo valor
no varía, siempre toma un mismo valor  .
.
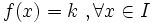
Tutorial en el que se explica el estudio del crecimiento de una función dada su gráfica.
Tutorial en el que se explica el estudio del crecimiento de una función dada su gráfica.
Conceptos de función creciente, decreciente y constante.
Estudio del crecimiento de una función a partir de su gráfica.
Estudio del crecimiento de una función a partir de su gráfica.
Estudio del crecimiento de una función a partir de su gráfica.
Estudio del crecimiento de una función a partir de su gráfica.
Actividades con las que aprenderás a determinar los intervalos de crecimiento y decrecimiento de una función.
En esta escena podrás ver cuando una función es creciente, decreciente o constante.
Determina los intervalos de crecimiento y decrecimiento de una función.
Se llama variación de una función  en un intervalo
en un intervalo ![[a,b]\;](/wikipedia/images/math/9/a/e/9ae0a6959368a1b0c6be4a9feb1e9b5c.png) , a lo que varía la variable dependiente de un extremo a otro del intervalo:
, a lo que varía la variable dependiente de un extremo a otro del intervalo:
![\Delta f_{[a,b]}=f(b)-f(a)\;](/wikipedia/images/math/f/1/e/f1ebdfa1d125fb540c0cf9d9b00d9152.png)
Extremos relativos: Máximos y mínimos
- Una función
 tiene un máximo relativo en un punto
tiene un máximo relativo en un punto 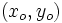 cuando
cuando 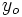 es mayor que los valores que toma la variable
es mayor que los valores que toma la variable  en un intervalo entorno al punto.
en un intervalo entorno al punto.
- Una función
 tiene un mínimo relativo en un punto
tiene un mínimo relativo en un punto 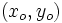 cuando
cuando 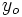 es menor que los valores que toma la variable
es menor que los valores que toma la variable  en un intervalo entorno al punto.
en un intervalo entorno al punto.
Tutorial en el que se explica el estudio de máximos y mínimos (relativos y absolutos) de una función dada su gráfica.
Tutorial en el que se explica el estudio de máximos y mínimos (relativos y absolutos) de una función dada su gráfica.
Conceptos de máximo y mínimo relativos.
Estudio de los puntos extremos de una función a partir de su gráfica.
Estudio de los puntos extremos de una función a partir de su gráfica.
Estudio de los puntos extremos de una función a partir de su gráfica.
Estudio de los puntos extremos de una función a partir de su gráfica.
Actividades con las que aprenderás a determinar los máximos y mínimos de una función dada gráficamente.
En esta escena podrás ver cuando una función alcanza un máximo o un mínimo.
Interpreta la siguiente gráfica que muestra las temperaturas a lo largo de un día de invierno en un pueblo de Valladolid. Averigua sus máximos y mínimos relativos.
Construye una gráfica que cumpla ciertas condiciones sobre los puntos por los que pasa. Se exigira, por ejemplo, que tenga máximos o mínimos en ciertos puntos, que tenga ciertos puntos de corte con los ejes, etc.
Unos alumnos de E.S.O. disponen de una cuerda de 80 metros de longitud con la que quieren construir rectángulos en el patio de su centro.
- Haz una tabla de valores donde se relacione la base de los rectángulos y su área.
- Representa gráficamente la función.
- Halla una expresión que te permita calcular el área de cualquiera de esos rectángulos, conocida su base.
- ¿Cuál es el dominio de esta función?
- ¿Para qué valor del lado se consigue un rectángulo de área máxima? ¿Qué tiene de peculiar ese valor?
Máximos y mínimos relativos o locales.
Máximos y mínimos absolutos.
Ejercicios
|
Ejercicios: Crecimiento. Máximos y mínimos |
Tendencias
Decimos que una función  tiende a un valor
tiende a un valor 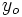 cuando la variable independiente tiende a un valor
cuando la variable independiente tiende a un valor 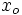 , si los valores de la variable
, si los valores de la variable  se acercan a
se acercan a 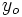 cuando la variable
cuando la variable  se acerca a
se acerca a 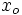 .
.
Simbólicamente:
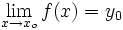
En la anterior expresión la tendencia de la variable independiente puede ser a  o
o  en vez de
en vez de 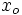 . Igualmente, la tendencia de la variable dependiente puede ser a
. Igualmente, la tendencia de la variable dependiente puede ser a  y
y  en vez de a un valor
en vez de a un valor 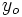 .
.
Así cuando, por ejemplo, la variable  se haga infinitamente grande y los correspondientes valores de la función se acerquen a un valor
se haga infinitamente grande y los correspondientes valores de la función se acerquen a un valor 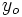 , escribiremos:
, escribiremos:
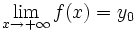
En esta escena podrás estudiar la tendencia de una función que relaciona la temperatura de un recipiente de agua que se va enfriando y el tiempo que ha transcurrido.
Estudia la tendencia del crecimiento de una población de búhos:
En ocasiones nos interesa saber cómo se comporta la función cuando la variable independiente aumenta mucho o disminuye mucho o cuando se acerca a una valor concreto. A los valores a los que se aproxima es lo que llamamos tendencia de la función. Observa la gráfica de la población de búhos (en miles) en un territorio en función del tiempo. Mueve el punto P para ayudarte a contestar las preguntas:
a) ¿Cuál es ese valor? (Nota: En el eje Y, 1 cuadrito = 1 millar de búhos)
Lo mismo ocurre cuando se hace cada vez más negativa la variable independiente, aunque esta tendencia no es el mismo valor.
b) ¿Cuál es ese valor?
Estudia la tendencia de la siguiente función:
La tendencia de una función se estudiar también cuando la x se acerca a un número real en vez de a (+/-)infinito. En la escena siguiente recorre la función con el punto P y apunta en tu cuaderno las tendencias de la función.
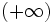 ?
?
b) ¿Y si x se hace muy grande negativamente, es decir, se aproxima a  ?
?
c) ¿A qué valor tiende la función cuando nos aproximamos a 2?
Estudio de las tendencias de una función a partir de su gráfica.
Estudio de las tendencias de una función a partir de su gráfica.
Estudio de las tendencias de una función a partir de su gráfica.
Estudio de las tendencias de una función a partir de su gráfica.
|
Actividad: Tendencia de una función
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Ejercicio Resuelto: Tendencia de una función
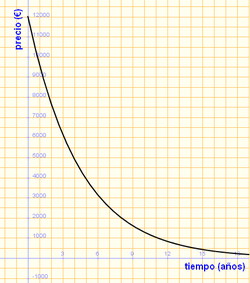
1. Compramos un coche por 12.000 €, y cada año que pasa su precio se devalua un 20%.
- a) Haz una tabla que exprese el precio del coche durante los próximos años.
- b) Representa gráficamente los resultados del apartado a).
- c) Encuentra una fórmula que exprese esta función.
- d) ¿Cómo es la variable independiente: continua o discreta?
- e) ¿Cuál es el dominio de esta función?. ¿Y su imagen?
- f) ¿Cual es la tendencia de esta función segun pasan los años?
- g) Describe el crecimiento e indica si tiene máximos o mínimos.
- a) Tabla de valores:
| x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| y | 12.000 | 9.600 | 7.680 | 6.144 | 4.915,2 | 3.932,2 | 3.145,7 | 2.516,6 |
- b) Representación gráfica:
- c) Continua.
- d)
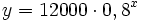 (€)
(€)
- e)
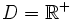 ;
; 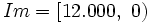 .
.
- f) La función tiende a 0 a medida que transcurre el tiempo.
- g) Es decreciente en todo su dominio. Tiene un máximo en x = 0 y no tiene mínimos.
- h) No es periódica.
Periodicidad
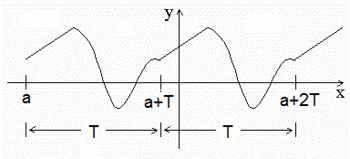
Una función es periódica si su gráfica se va repitiendo a intervalos. Al menor valor posible, T, de la longitud de dicho intervalo, se le llama periodo. Se cumple: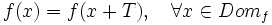 |
Actividades con las que aprenderás a determinar si una función es periódica y a hallar su período a partir de su gráfica.
|
Actividad: Funciones periódicas
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Estudio de la periodicidad de una función dada por una gráfica.
Simetrías
Continuidad
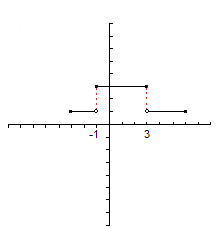
Cuando la gráfica de una función tiene saltos bruscos (no se puede dibujar de un solo trazo) decimos que es discontinua. En caso contrario se dice que es continua. Los puntos donde se producen los saltos se llaman discontinuidades.
|
Actividad interactiva: Continuidad
1. Autoevaluación.
Actividad: |
Ejercicios
|
Ejercicios: Continuidad |
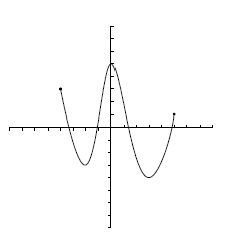
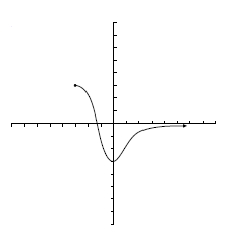
![[-4, -2]\;\!](/wikipedia/images/math/1/6/e/16e23fb49812889eb7e588de4087f56b.png) la función es decreciente, en
la función es decreciente, en ![[-2, 0]\;\!](/wikipedia/images/math/9/5/1/951cb0affc7e6701b581d84cd1a412cf.png) es creciente, en
es creciente, en ![[0, 3]\;\!](/wikipedia/images/math/0/a/0/0a0f42dd2994b25130f2ff46613824e5.png) es decreciente y en
es decreciente y en ![[3, 5]\;\!](/wikipedia/images/math/7/6/7/7676542397cfbd4e5845abca88f05d64.png) creciente.
creciente.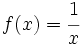 . cuando
. cuando