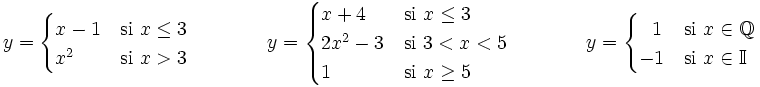Plantilla:Funciones definidas a trozos
De Wikipedia
| Revisión de 12:19 21 ene 2009 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 12:20 21 ene 2009 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 15: | Línea 15: | ||
| <center><math>y = \begin{cases} x+4 & \mbox{si }x \le 3 \\ 7-2(x-3) & \mbox{si }3<x<6 \\ 1 & \mbox{si }x \ge 6 \end{cases}</math></center> | <center><math>y = \begin{cases} x+4 & \mbox{si }x \le 3 \\ 7-2(x-3) & \mbox{si }3<x<6 \\ 1 & \mbox{si }x \ge 6 \end{cases}</math></center> | ||
| - | Mueve el punto P para ver que función corresponde a cada tramo. | + | Mueve el punto P para ver que expresión corresponde a cada tramo. |
| <center><iframe> | <center><iframe> | ||
Revisión de 12:20 21 ene 2009
Una función definida a trozos es aquella que utiliza varias expresiones para su definición, utilizando cada una de ellas en un determinado tramo del dominio de definición de la función principal.
Son funciones definidas a trozos:
 Actividad Interactiva: Funciones definidas a trozos
Actividad 1: Ejemplo de función definida a trozos.
Actividad: En la siguiente escena puedes ver la representación de la función  Mueve el punto P para ver que expresión corresponde a cada tramo. |
Ejemplo: Función definida a trozos
Representa la siguiente función:
Para su representación, tenemos que dibujar cada una de las tres funciones en sus respectivos tramos, prestando especial atención a los puntos de "empalme" (extremos de los intervalos de definición).
Actividad Interactiva: Funciones definidas a trozos
Actividad 1: Funciones lineales definidas en dos trozos.
Actividad: En esta escena representaremos funciones a trozos del tipo:  Modifica con los controles los valores de a, b, c, d y k. Podrás obtener así distintas funciones a trozos. |
