Transformaciones elementales de funciones (1ºBach)
De Wikipedia
| Revisión de 08:56 23 ene 2009 Coordinador (Discusión | contribuciones) (→Simetría respecto del eje X) ← Ir a diferencia anterior |
Revisión de 09:00 23 ene 2009 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 55: | Línea 55: | ||
| }} | }} | ||
| }} | }} | ||
| + | {{p}} | ||
| + | ==Traslación horizontal== | ||
| + | {{Caja_Amarilla|texto=Sea <math>f(x)\;</math> una función y <math>k>0\;</math> un número real, entonces la gráfica de la función <math>f(x+k)\;</math> se obtiene a partir de la de <math>f(x)\;</math> desplazándola <math>k\;</math> unidades hacia la izquierda y la de <math>f(x-k)\;</math> desplazándola <math>k\;</math> unidades hacia la derecha.}} | ||
| + | {{p}} | ||
| + | {{AI2|titulo=Actividad Interactiva: ''Traslación horizontal de una función''|cuerpo= | ||
| + | {{ai_cuerpo | ||
| + | |enunciado='''Actividad 1.''' Representación gráfica de una función <math>f(x)\;</math> cualquiera y de su transformada <math>f(x \pm k)</math>. | ||
| + | |actividad= | ||
| + | En esta escena tienes la gráfica de la función <math>f(x) = x^2\;</math> (en verde) y la de <math>f(x+1)=(x+1)^2\;</math> (en amarillo). | ||
| + | |||
| + | Prueba a cambiar el valor de <math>k\;</math>: <math>f(x+2)=(x+2)^2 \ , \ f(x)-3=(x-3)^2</math>. Compáralas con <math>f(x)\;</math>. | ||
| + | |||
| + | Prueba a cambiar también la función <math>f(x)=x^2\;</math> por otras funciones, por ejemplo, <math>f(x)=x^3\;</math>. | ||
| + | |||
| + | No olvides pulsar "Intro" al cambiar cada función. | ||
| + | |||
| + | {{p}} | ||
| + | <center><iframe> | ||
| + | url=http://maralboran.org/web_ma/descartes/Analisis/El_pinta_graficas/grafic_4c.html | ||
| + | width=420 | ||
| + | height=360 | ||
| + | name=myframe | ||
| + | </iframe></center> | ||
| + | <center>[http://maralboran.org/web_ma/descartes/Analisis/El_pinta_graficas/grafic_4c.html '''Click''' aquí si no se ve bien la escena]</center> | ||
| + | }} | ||
| + | }} | ||
| + | {{p}} | ||
| [[Categoría: Matemáticas]][[Categoría: Funciones]] | [[Categoría: Matemáticas]][[Categoría: Funciones]] | ||
Revisión de 09:00 23 ene 2009
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | Test de Álgebra | WIRIS Geogebra Calculadoras |
Traslación vertical
Sea  una función y
una función y 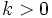 un número real, entonces la gráfica de la función
un número real, entonces la gráfica de la función 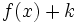 se obtiene a partir de la de
se obtiene a partir de la de  desplazándola
desplazándola  unidades hacia arriba y la de
unidades hacia arriba y la de 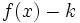 desplazándola
desplazándola  unidades hacia abajo.
unidades hacia abajo.
|
Actividad Interactiva: Traslación vertical de una función
Actividad 1. Representación gráfica de una función
 cualquiera y de su transformada cualquiera y de su transformada 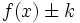 . .Actividad: En esta escena tienes la gráfica de la función  (en verde) y la de (en verde) y la de 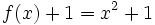 (en amarillo). (en amarillo).
Prueba a cambiar el valor de Prueba a cambiar también la función No olvides pulsar "Intro" al cambiar cada función. |
Simetría respecto del eje X
Las gráficas de las funciones  y su opuesta,
y su opuesta, 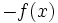 , son simétricas respecto del eje de abscisas.
, son simétricas respecto del eje de abscisas.
|
Actividad Interactiva: Función simétrica respecto del eje X
Actividad 1. Representación gráfica de una función
 cualquiera y de su simétrica cualquiera y de su simétrica 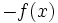 . .Actividad: En esta escena tienes la gráfica de la función 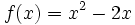 (en verde) y la de su simétrica (en verde) y la de su simétrica 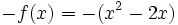 (en amarillo). (en amarillo).
Prueba a cambiar la función No olvides pulsar "Intro" al cambiar cada función. |
Traslación horizontal
Sea  una función y
una función y 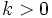 un número real, entonces la gráfica de la función
un número real, entonces la gráfica de la función 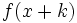 se obtiene a partir de la de
se obtiene a partir de la de  desplazándola
desplazándola  unidades hacia la izquierda y la de
unidades hacia la izquierda y la de 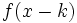 desplazándola
desplazándola  unidades hacia la derecha.
unidades hacia la derecha.
|
Actividad Interactiva: Traslación horizontal de una función
Actividad 1. Representación gráfica de una función
 cualquiera y de su transformada cualquiera y de su transformada 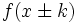 . .Actividad: En esta escena tienes la gráfica de la función  (en verde) y la de (en verde) y la de 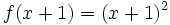 (en amarillo). (en amarillo).
Prueba a cambiar el valor de Prueba a cambiar también la función No olvides pulsar "Intro" al cambiar cada función. |
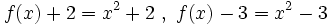 . Compáralas con
. Compáralas con 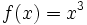 .
.
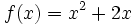 por otras funciones, por ejemplo,
por otras funciones, por ejemplo, 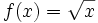 . (Para la raíz cuadrada debes escribir sqrt(x)).
. (Para la raíz cuadrada debes escribir sqrt(x)).
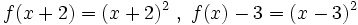 . Compáralas con
. Compáralas con 
