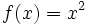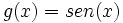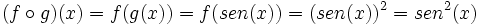Composición de funciones (1ºBach)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 17:01 24 ene 2009 Coordinador (Discusión | contribuciones) (→Función compuesta) ← Ir a diferencia anterior |
Revisión de 17:59 26 ene 2009 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 61: | Línea 61: | ||
| Obsérvese que las funciones obtenidas en ambos apartados son distintas. El orden en que se efectúe la composición afecta al resultado. | Obsérvese que las funciones obtenidas en ambos apartados son distintas. El orden en que se efectúe la composición afecta al resultado. | ||
| }} | }} | ||
| - | + | {{p}} | |
| + | ==Videos sobre composición de funciones== | ||
| + | {{Video2b | ||
| + | |titulo1=Composición de funciones | ||
| + | |duracion=4'54" | ||
| + | |sinopsis=Video tutorial de matematicasbachiller.com | ||
| + | |url1=http://www.matematicasbachiller.com/videos/cdiferencial/df_t_01/vdf0138.htm | ||
| + | }} | ||
| + | {{p}} | ||
| + | ===Ejercicios (videos)=== | ||
| + | {{ejercicio | ||
| + | |titulo=Ejercicios: ''Composición de funciones'' | ||
| + | |cuerpo= | ||
| + | ::*[http://www.matematicasbachiller.com/videos/cdiferencial/df_t_01/vdf0138_01.htm Ejercicio 1] | ||
| + | ::*[http://www.matematicasbachiller.com/videos/cdiferencial/df_t_01/vdf0138_02.htm Ejercicio 2] | ||
| + | }} | ||
| [[Categoría: Matemáticas]][[Categoría: Funciones]] | [[Categoría: Matemáticas]][[Categoría: Funciones]] | ||
Revisión de 17:59 26 ene 2009
Menú:
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
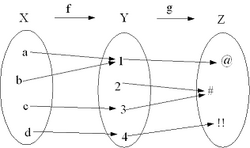
Función compuesta
| La función compuesta es una función formada por la aplicación sucesiva de otras dos funciones. Formalmente:
Dadas dos funciones 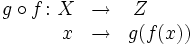 Se aplica sobre el argumento la función más próxima al mismo, y al resultado del cálculo anterior se le aplica finalmente la función restante. 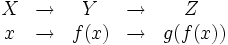 La expresión |
Ejemplo: Composición de funciones
Dadas las funciones
- a) Halla la función
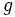 compuesta con
compuesta con  .
.
- b) Halla la función
 compuesta con
compuesta con 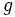 .
.
- a) Halla la función
Solución:
a) La función 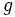 compuesta con
compuesta con  es:
es:
b) La función  compuesta con
compuesta con 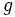 es:
es:
Videos sobre composición de funciones
Ejercicios (videos)
|
Ejercicios: Composición de funciones |
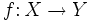 y
y 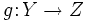 , donde la imagen de
, donde la imagen de 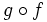 se lee f compuesta con g. Nótese que se nombra, no siguiendo el orden de escritura, sino el orden en que se aplican las funciones a su argumento.
se lee f compuesta con g. Nótese que se nombra, no siguiendo el orden de escritura, sino el orden en que se aplican las funciones a su argumento.