Fórmulas trigonométricas (1ºBach)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 17:24 3 mar 2009 Coordinador (Discusión | contribuciones) (→Razones trigonométricas de la suma de dos ángulos) ← Ir a diferencia anterior |
Revisión de 17:49 3 mar 2009 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 54: | Línea 54: | ||
| ==Razones trigonométricas de la diferencia de dos ángulos== | ==Razones trigonométricas de la diferencia de dos ángulos== | ||
| + | {{Teorema|titulo=Razones trigonométricas de la diferencia de dos ángulos | ||
| + | |enunciado= | ||
| + | :'''II.1:'''{{b4}}<math>sen \, (\alpha - \beta) = sen \, \alpha \cdot cos \, \beta - cos \, \alpha \cdot sen \, \beta</math> | ||
| + | |||
| + | :'''II.2:'''{{b4}}<math>cos \, (\alpha - \beta) = cos \, \alpha \cdot cos \, \beta + sen \, \alpha \cdot sen \, \beta</math> | ||
| + | |||
| + | :'''II.3:'''{{b4}}{{sube|porcentaje=+10%|contenido=<math>tg \, (\alpha - \beta) = \frac{tg \, \alpha - tg \, \beta}{1 + tg \, \alpha \cdot tg \, \beta}</math>}} | ||
| + | |demo= | ||
| + | Para las demostraciones basta sustituir \alpha - \beta por \alpha + (-\beta) y aplicar las fórmulas de la suma (I.1, I.2 y I.3) y tener en cuenta las relaciones entre las razones trigonométricas de un ángulo y su opuesto: | ||
| + | <center><math>sen \, (-\alpha)=-sen \, \alpha \, , \quad cos \, (-\alpha)=cos \, \alpha \, , \quad tg \, (-\alpha)=-tg \, \alpha</math></center> | ||
| + | }} | ||
| {{p}} | {{p}} | ||
| ==Razones trigonométricas del ángulo doble== | ==Razones trigonométricas del ángulo doble== | ||
Revisión de 17:49 3 mar 2009
Menú:
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
Razones trigonométricas de la suma de dos ángulos
Razones trigonométricas de la suma de dos ángulos
- I.1:
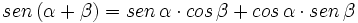
- I.2:
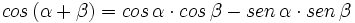
- I.3:
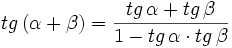
Razones trigonométricas de la diferencia de dos ángulos
Razones trigonométricas de la diferencia de dos ángulos
- II.1:
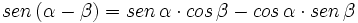
- II.2:
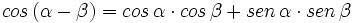
- II.3:
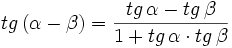
Demostración:
Para las demostraciones basta sustituir \alpha - \beta por \alpha + (-\beta) y aplicar las fórmulas de la suma (I.1, I.2 y I.3) y tener en cuenta las relaciones entre las razones trigonométricas de un ángulo y su opuesto:
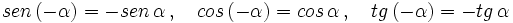
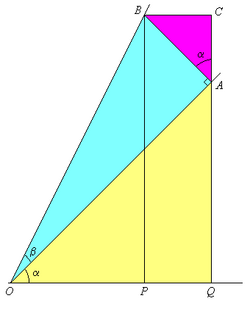
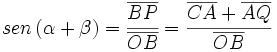
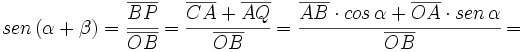
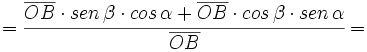
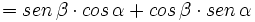
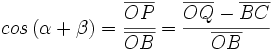
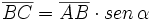
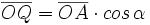
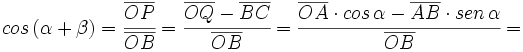
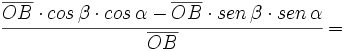
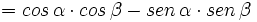
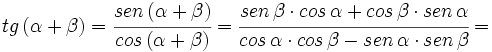
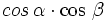 )
)


