Números complejos: Definición (1ºBach)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 19:45 4 mar 2009 Coordinador (Discusión | contribuciones) (→Opuesto y conjugado de un complejo) ← Ir a diferencia anterior |
Revisión de 19:51 4 mar 2009 Coordinador (Discusión | contribuciones) (→Forma binómica de un número complejo) Ir a siguiente diferencia → |
||
| Línea 50: | Línea 50: | ||
| ===Forma binómica de un número complejo=== | ===Forma binómica de un número complejo=== | ||
| {{Caja_Amarilla|texto= | {{Caja_Amarilla|texto= | ||
| - | *La expresión <math>a+bi\,</math> se denomina '''forma binómica''' de un número complejo. En ella, a <math>a\,</math> se le llama '''parte real''' y a <math>b\,</math> '''parte imaginaria'''. | + | *La expresión <math>a+bi\,</math> se denomina '''forma binómica''' de un número complejo. En ella, a <math>a\,</math> se le llama '''parte real''' y a <math>b\,</math> '''parte imaginaria'''. Si escribimos <math>z=a+bi\,</math>, entonces se dice que <math>Re(z)=a\,</math> y <math>Im(z)=b\,</math> |
| *Si <math>b=0\,</math>, lo que tenemos es un número real, por tanto <math>\mathbb{R} \sub \mathbb{C}</math>. | *Si <math>b=0\,</math>, lo que tenemos es un número real, por tanto <math>\mathbb{R} \sub \mathbb{C}</math>. | ||
| *Si <math>b \ne 0\,</math>, lo que tenemos no es un número real, es un número '''imaginario'''. | *Si <math>b \ne 0\,</math>, lo que tenemos no es un número real, es un número '''imaginario'''. | ||
Revisión de 19:51 4 mar 2009
Menú:
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
Necesidad de ampliación del campo numérico
Hay ecuaciones como
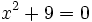
que no tienen solución en el conjunto de los números reales
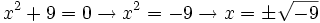 (no existe en
(no existe en  )
)Vamos a definir un nuevo conjunto que amplie al conjunto de los números reales y en el cual estas ecuaciones si tengan solución. Ese conjunto va a ser el conjunto de los números complejos. Para ello vamos a empezar dando sentido a las raíces de números negativos.
Unidad imaginaria
Se denomina unidad imaginaria a 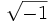 . Se designa por la letra
. Se designa por la letra 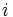
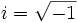
Con esta definición, la ecuación anterior ahora si tiene solución "imaginaria":
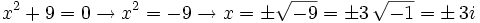
Potencias de la unidad imaginaria
A partir de 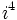 se repiten cíclicamente los valores.
se repiten cíclicamente los valores.
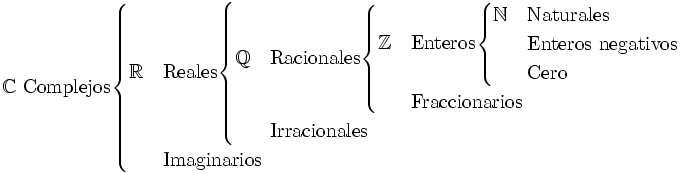
El conjunto de los números complejos
Definimos el conjunto de los números complejos de la siguiente manera:
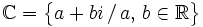
Forma binómica de un número complejo
- La expresión
 se denomina forma binómica de un número complejo. En ella, a
se denomina forma binómica de un número complejo. En ella, a  se le llama parte real y a
se le llama parte real y a  parte imaginaria. Si escribimos
parte imaginaria. Si escribimos 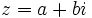 , entonces se dice que
, entonces se dice que 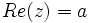 y
y 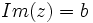
- Si
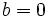 , lo que tenemos es un número real, por tanto
, lo que tenemos es un número real, por tanto 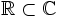 .
.
- Si
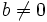 , lo que tenemos no es un número real, es un número imaginario.
, lo que tenemos no es un número real, es un número imaginario.
- Si
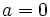 y
y 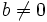 , se le llama número imaginario puro.
, se le llama número imaginario puro.
- Dos números complejos en forma binómica son iguales si tienen iguales sus partes reeales y sus partes imaginarias.
Opuesto y conjugado de un complejo
- Se define el opuesto de un complejo
 como el número complejo
como el número complejo 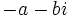 .
.
- Se define el conjugado de un complejo
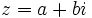 como el número complejo
como el número complejo 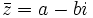 .
.
Proposición
- Cualquier ecuación de segundo grado con coeficientes reales que no tenga solución real tiene dos soluciones imaginarias que son números complejos conjugados
Demostración:
Veámoslo con un ejemplo:
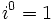
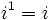
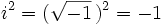
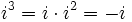
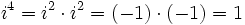
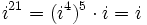 (Al hacer la división entera:
(Al hacer la división entera: 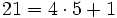 ).
).
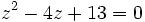
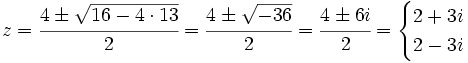
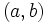 representa las coordenadas de un punto del plano. Diremos que
representa las coordenadas de un punto del plano. Diremos que 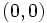 y extremo
y extremo