Números complejos: Operaciones en forma polar (1ºBach)
De Wikipedia
| Revisión de 10:03 12 mar 2009 Coordinador (Discusión | contribuciones) (→Multiplicación de números complejos en forma polar) ← Ir a diferencia anterior |
Revisión de 10:12 12 mar 2009 Coordinador (Discusión | contribuciones) (→Potencias de números complejos en forma polar) Ir a siguiente diferencia → |
||
| Línea 35: | Línea 35: | ||
| ==Potencias de números complejos en forma polar== | ==Potencias de números complejos en forma polar== | ||
| - | {{Caja_Amarilla|texto=La potencia n-ésima de un compejo es el resultado de multiplicar dicho complejo por sí mismo n veces, por tanto, aplicando la fórmula del producto: | + | {{Teorema|titulo=Potencia de un complejo en forma polar|enunciado=:La potencia n-ésima de un compejo se obtiene de la siguiente manera: |
| - | <center><math>(r_\alpha)^n =(r_\alpha) \cdot (r_\alpha) \cdot \cdots \cdot (r_\alpha)=(r \cdot r \cdots r)_{( \alpha + \alpha + \cdots + \alpha )}=(r^n)_{n \cdot \alpha}</math></center> | + | {{Caja|contenido=<math>(r_\alpha)^n =(r^n)_{n \cdot \alpha}</math>}} |
| + | |demo=La potencia n-ésima de un compejo es el resultado de multiplicar dicho complejo por sí mismo n veces, por tanto, aplicando la fórmula del producto: | ||
| + | |||
| + | :<math>(r_\alpha)^n =(r_\alpha) \cdot (r_\alpha) \cdot \cdots \cdot (r_\alpha)=(r \cdot r \cdots r)_{( \alpha + \alpha + \cdots + \alpha )}=(r^n)_{n \cdot \alpha}</math> | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| Línea 67: | Línea 70: | ||
| :Esta fórmula debe su nombre al matemático francés [[Moivre| Abraham de Moivre]] (1667-1754). | :Esta fórmula debe su nombre al matemático francés [[Moivre| Abraham de Moivre]] (1667-1754). | ||
| |demo= | |demo= | ||
| - | Basta aplicar la fórmula de la potencia de un complejo en forma polar y tener en cuenta la forma trigonométrica de un número complejo. | + | Basta aplicar la fórmula de la potencia de un complejo en forma polar y tener en cuenta la forma trigonométrica de un número complejo: |
| + | |||
| + | :<math>(cos \, \alpha + i \, sen \, \alpha)^n=(1_\alpha)^n=(1^n)_{n \cdot \alpha}=1_{n \cdot \alpha}=cos \, (n \, \alpha) + i \, sen \, (n \, \alpha)</math> | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión de 10:12 12 mar 2009
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
Multiplicación de números complejos en forma polar
Producto de complejos en forma polar
El producto de dos numeros complejos en forma polar es otro complejo en forma polar cuyo módulo es el producto de los módulos y el argumento la suma de los argumentos de los respectivos complejos.
|
|
|
Actividad interactiva: Multiplicación de complejos en forma polar
|
Potencias de números complejos en forma polar
Potencia de un complejo en forma polar
- La potencia n-ésima de un compejo se obtiene de la siguiente manera:
|
|
La potencia n-ésima de un compejo es el resultado de multiplicar dicho complejo por sí mismo n veces, por tanto, aplicando la fórmula del producto:
|
Actividad interactiva: Potencias de complejos en forma polar
|
Fórmula de Moivre
Fórmula de Moivre
Basta aplicar la fórmula de la potencia de un complejo en forma polar y tener en cuenta la forma trigonométrica de un número complejo:
División de números complejos en forma polar
|
Actividad interactiva: División de complejos en forma polar
|
Radicación de números complejos en forma polar
|
Actividad interactiva: Raíces de complejos en forma polar
|
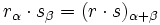
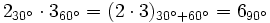

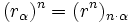
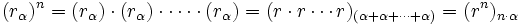
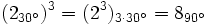
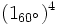 b)
b)  c)
c) 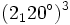 d)
d) 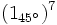
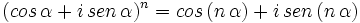
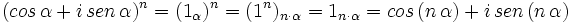

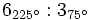
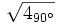 b)
b) ![\sqrt[3]{8_{120^\circ}}](/wikipedia/images/math/0/2/9/02928c662b770c320d65ec6f6ebb988d.png) c)
c) ![\sqrt[5]{5_{270^\circ}}](/wikipedia/images/math/a/a/9/aa96d66344414293e64e280028494f05.png) d)
d) ![\sqrt[4]{6_{120^\circ}}](/wikipedia/images/math/5/b/2/5b29523f5dc1a2d4bbc07a377e06bae8.png)

