Vectores: Definición y operaciones (1ºBach)
De Wikipedia
| Revisión de 09:21 13 mar 2009 Coordinador (Discusión | contribuciones) (→Vectores equipolentes. Vectores libres) ← Ir a diferencia anterior |
Revisión de 16:15 13 mar 2009 Coordinador (Discusión | contribuciones) (→Producto de un vector por un número) Ir a siguiente diferencia → |
||
| Línea 90: | Línea 90: | ||
| ===Producto de un vector por un número=== | ===Producto de un vector por un número=== | ||
| + | {{Caja_amarilla|El producto de un número real k por un vector v es otro vector <math>kv</math> que tiene las siguientes características: | ||
| + | |||
| + | *'''Módulo:''' <math>|kv|=|k| \cdot |v|</math> | ||
| + | *'''Dirección:''' la misma que v. | ||
| + | *'''Sentido:''' el mismo que v si k>0 y opuesto si k<0. | ||
| + | }} | ||
| ===Suma y resta de vectores=== | ===Suma y resta de vectores=== | ||
Revisión de 16:15 13 mar 2009
Tabla de contenidos[esconder] |
Vectores fijos
Un vector fijo es un segmento orientado que queda determinado por un punto origen, A y otro punto extremo, B. Lo simbolizamos Características de un vector:
| 
|
Vectores equipolentes. Vectores libres
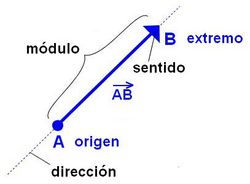
Dos vectores son equipolentes cuando tienen el mismo módulo, dirección y sentido (aunque sus orígenes y extremos sean distintos)
Dado un vector, existen infinitos vectores equipolentes a él. Cuando queremos hacer uso de un vector podemos elegir uno de esos infinitos vectores iguales a él y utilizarlo como representante del vector. Al conjunto de todos los vectores equipolentes a uno dado se le llama vector libre. Un vector libre lo denotaremos mediante una letra con una flecha: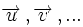 
 Actividad interactiva: Vectores Actividad 1: Módulo, dirección y sentido de un vector fijo. Actividad 2: Vectores equipolentes. Actividad:[Mostrar]
Actividad 3: Vectores libres. |
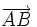
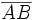
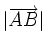
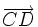son equipolentes. Para ello pincha y arrastra los puntitos amarillos que ves en A y B.
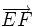y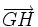 
son equipolentes.
