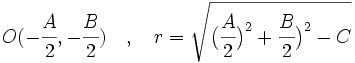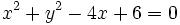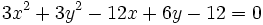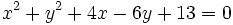La circunferencia (1ºBach)
De Wikipedia
| Revisión de 23:07 23 mar 2009 Coordinador (Discusión | contribuciones) (→Ecuación de la circunferencia) ← Ir a diferencia anterior |
Revisión de 23:08 23 mar 2009 Coordinador (Discusión | contribuciones) (→Ecuación de la circunferencia) Ir a siguiente diferencia → |
||
| Línea 54: | Línea 54: | ||
| {{AI2|titulo=Actividad Interactiva: ''Ecuación de la circunferencia''|cuerpo= | {{AI2|titulo=Actividad Interactiva: ''Ecuación de la circunferencia''|cuerpo= | ||
| {{ai_cuerpo | {{ai_cuerpo | ||
| - | |enunciado='''Actividad 1:''' En esta escena vamos a hallar la ecuación de la circunferencia de centro<math>O(-3,0)\,</math> y radio <math>r=5\,</math>. | + | |enunciado='''Actividad 1:''' En esta escena vamos a hallar la ecuación de la circunferencia de centro <math>O(-3,0)\,</math> y radio <math>r=5\,</math>. |
| |actividad=Hallamos la ecuación de la cirecunferencia: | |actividad=Hallamos la ecuación de la cirecunferencia: | ||
| Línea 67: | Línea 67: | ||
| name=myframe | name=myframe | ||
| </iframe></center> | </iframe></center> | ||
| - | <center>[http://maralboran.org/web_ma/descartes/Bach_CNST_1/Geometria_afin_analitica_plano_lugares_geometricos/Geometria_4_1.html '''Click''' aquí si no se ve bien la escena]</center> | + | <center>[http://maralboran.org/web_ma/descartes/Bach_CNST_1/Geometria_afin_analitica_plano_lugares_geometricos/Geometria_8_4.html '''Click''' aquí si no se ve bien la escena]</center> |
| '''Ejercicio:''' | '''Ejercicio:''' | ||
| Línea 73: | Línea 73: | ||
| De las siguientes ecuaciones, indica cuales son circunferencias y cuales no: | De las siguientes ecuaciones, indica cuales son circunferencias y cuales no: | ||
| - | # x^2+y^2-4x+6=0 | + | # <math>x^2+y^2-4x+6=0\,</math> |
| - | # 3x^2+3y^2-12x+6y-12=0 | + | # <math>3x^2+3y^2-12x+6y-12=0\,</math> |
| - | # x^2+y^2+4x-6y+13=0 | + | # <math>x^2+y^2+4x-6y+13=0\,</math> |
| Ayúdate de la escena para comprobarlo. Para ello debes editar la ecuación que aparece en rojo. | Ayúdate de la escena para comprobarlo. Para ello debes editar la ecuación que aparece en rojo. | ||
Revisión de 23:08 23 mar 2009
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Circunferencia
La circunferencia de centro  y radio
y radio  , es el lugar geométrico de los puntos
, es el lugar geométrico de los puntos 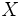 , cuya distancia al centro es
, cuya distancia al centro es  .
.
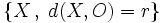
Ecuación de la circunferencia
De la anterior definición, utilizando la fórmula de la distancia entre dos puntos, tenemos:
La ecuación de la circunferencia de centro 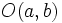 y radio
y radio  , es:
, es:
|
|
Proposición
La ecuación de una circunferencia de centro 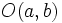 y radio
y radio  , es:
, es:
|
|
donde: 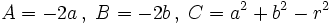 .
.
Partiendo de la ecuación de la circunferencia:

Elevando al cuadrado ambos términos:
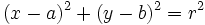
y desarrollando el radicando:
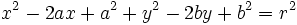
Agrupando términos:
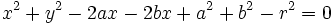
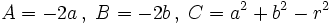 , se tiene la ecuación.
, se tiene la ecuación.Corolario
Dada la circunferencia de ecuación 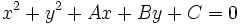 , su centro y su radio vienen dados por:
, su centro y su radio vienen dados por:
|
|
Es inmediato a partir de la proposición anterior, despejando
 ,
,  y
y  .
.|
Actividad Interactiva: Ecuación de la circunferencia
Actividad 1: En esta escena vamos a hallar la ecuación de la circunferencia de centro
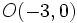 y radio y radio 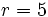 . .Actividad: Hallamos la ecuación de la cirecunferencia: Su representación gráfica puedes verla en esta escena: Ejercicio: De las siguientes ecuaciones, indica cuales son circunferencias y cuales no: |