La circunferencia (1ºBach)
De Wikipedia
| Revisión de 18:16 24 mar 2009 Coordinador (Discusión | contribuciones) (→Posiciones relativas de una recta y de una circunferencia) ← Ir a diferencia anterior |
Revisión de 18:17 24 mar 2009 Coordinador (Discusión | contribuciones) (→Posiciones relativas de una recta y de una circunferencia) Ir a siguiente diferencia → |
||
| Línea 101: | Línea 101: | ||
| {{AI2|titulo=Actividad Interactiva: ''Posición relativa de recta y circunferencia''|cuerpo= | {{AI2|titulo=Actividad Interactiva: ''Posición relativa de recta y circunferencia''|cuerpo= | ||
| {{ai_cuerpo | {{ai_cuerpo | ||
| - | |enunciado='''Actividad 1:''' En esta escena vamos a hallar la posición relativa de la recta <math>r: \, 2x-y+1=0</math> y una circunferencia <math>s: \, x^2+y^2-2x-2y-2=0</math>. | + | |enunciado='''Actividad 1:''' En esta escena vamos a hallar la posición relativa de la recta <math>r: \, 2x-y+1=0</math> y la circunferencia <math>s: \, x^2+y^2-2x-2y-2=0</math>. |
| |actividad= | |actividad= | ||
Revisión de 18:17 24 mar 2009
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Circunferencia
La circunferencia de centro  y radio
y radio  , es el lugar geométrico de los puntos
, es el lugar geométrico de los puntos 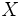 , cuya distancia al centro es
, cuya distancia al centro es  .
.
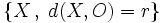
Ecuación de la circunferencia
De la anterior definición, utilizando la fórmula de la distancia entre dos puntos, tenemos:
La ecuación de la circunferencia de centro 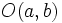 y radio
y radio  , es:
, es:
|
|
Proposición
La ecuación de una circunferencia de centro 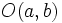 y radio
y radio  , es:
, es:
|
|
donde: 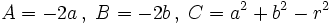 .
.
Partiendo de la ecuación de la circunferencia:

Elevando al cuadrado ambos términos:
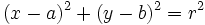
y desarrollando el radicando:
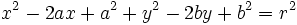
Agrupando términos:
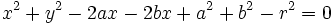
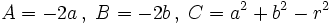 , se tiene la ecuación.
, se tiene la ecuación.Corolario
Dada la circunferencia de ecuación 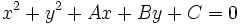 , su centro y su radio vienen dados por:
, su centro y su radio vienen dados por:
|
|
Es inmediato a partir de la proposición anterior, despejando
 ,
,  y
y  .
.|
Actividad Interactiva: Ecuación de la circunferencia
Actividad 1: En esta escena vamos a hallar la ecuación de la circunferencia de centro
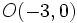 y radio y radio 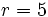 . .Actividad: Hallamos la ecuación de la cirecunferencia: 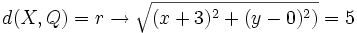 Elevando al cuadrado ambos miembros y desarrollando; 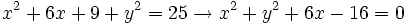
Ejercicio: Mueve el punto X a otro punto de la circunferencia y comprueba que sus coordenadas verifican su ecuación. Observa como el radio no varía. Nota: La ecuación de la circunferencia (en rojo) es editable. Prueba a cambiarla por otras ecuaciones de circunferencia para ver sus gráficas. |
Posiciones relativas de una recta y de una circunferencia
Una recta 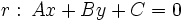 y una circunferencia
y una circunferencia 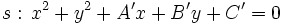 pueden ser:
pueden ser:
- Secantes: si se cortan en 2 puntos.
- Tangentes: si se cortan en un punto.
- Exteriores: si no se cortan.
Los puntos de corte se averiguan resolviendo el sistema: 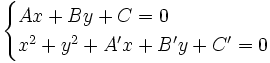
(Nota: Las ecuaciones de la recta y de la circunferencia nos las pueden dar en otra forma.)
|
Actividad Interactiva: Posición relativa de recta y circunferencia
Actividad 1: En esta escena vamos a hallar la posición relativa de la recta
 y la circunferencia y la circunferencia 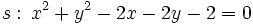 . .Actividad: Para poder comprobar los resultados en la escena, vamos a poner la ecuación de la recta en forma explícita,
Su representación gráfica puedes verla en la escena:
Los puntos de corte se averiguan resolviendo el sistema: 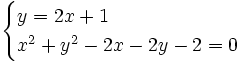 Lo resolvemos por sustitución: 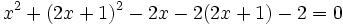 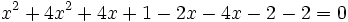 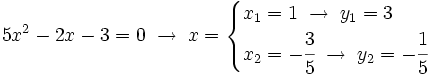 Los puntos de corte son:
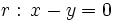 y la circunferencia y la circunferencia 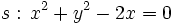 . . |

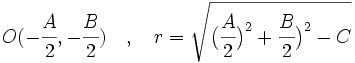
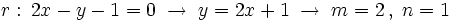
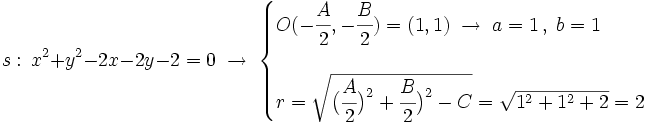
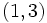 y
y