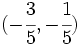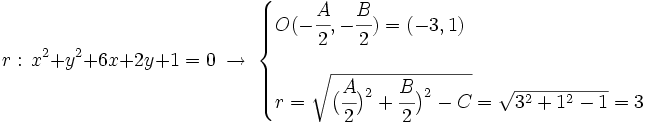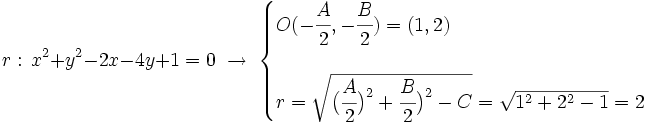La circunferencia (1ºBach)
De Wikipedia
| Revisión de 18:36 24 mar 2009 Coordinador (Discusión | contribuciones) (→Posiciones relativas de una recta y de una circunferencia) ← Ir a diferencia anterior |
Revisión de 18:52 24 mar 2009 Coordinador (Discusión | contribuciones) (→Posiciones relativas de dos circunferencias) Ir a siguiente diferencia → |
||
| Línea 160: | Línea 160: | ||
| {{p}} | {{p}} | ||
| ==Posiciones relativas de dos circunferencias== | ==Posiciones relativas de dos circunferencias== | ||
| - | {{Caja_Amarilla|texto=Dos circunferencias <math>r: \, x^2+y^2+Ax+By+C=0</math> y una circunferencia <math>s: \, x^2+y^2+A'x+B'y+C'=0</math> pueden ser: | + | {{Caja_Amarilla|texto=Dos circunferencias pueden ser: |
| [[Imagen:Circunferencias.png|160px|right]] | [[Imagen:Circunferencias.png|160px|right]] | ||
| Línea 177: | Línea 177: | ||
| *'''Coincidentes''', si tienen el mismo centro y el mismo radio. En realidad no se trata de dos circunferencias distintas, sino de una misma. Si dos circunferencias se cortan en más de dos puntos, necesariamente son circunferencias coincidentes. | *'''Coincidentes''', si tienen el mismo centro y el mismo radio. En realidad no se trata de dos circunferencias distintas, sino de una misma. Si dos circunferencias se cortan en más de dos puntos, necesariamente son circunferencias coincidentes. | ||
| - | Los puntos de corte se averiguan resolviendo el sistema: <math> | + | Si sus ecuaciones son: |
| + | |||
| + | <math> | ||
| \begin{cases} | \begin{cases} | ||
| - | x^2+y^2+Ax+By+C=0 | + | r: \; x^2+y^2+Ax+By+C=0 |
| \\ | \\ | ||
| - | x^2+y^2+A'x+B'y+C'=0 | + | s: \; x^2+y^2+A'x+B'y+C'=0 |
| \end{cases} | \end{cases} | ||
| </math> | </math> | ||
| + | los puntos de corte se averiguan resolviendo el sistema. | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| {{AI2|titulo=Actividad Interactiva: ''Posición relativa de dos circunferencias''|cuerpo= | {{AI2|titulo=Actividad Interactiva: ''Posición relativa de dos circunferencias''|cuerpo= | ||
| {{ai_cuerpo | {{ai_cuerpo | ||
| - | |enunciado='''Actividad 1:''' En esta escena vamos a hallar la posición relativa de las circunferencias <math>r: \, x^2+y^2+2x=0</math> y la circunferencia <math>s: \, x^2+y^2+2x-8y-26=0</math>. | + | |enunciado='''Actividad 1:''' En esta escena vamos a hallar la posición relativa de las circunferencias <math>r: \, x^2+y^2+6x+2y+1=0</math> y la circunferencia <math>s: \, x^2+y^2-2x-4y+1=0</math>. |
| |actividad= | |actividad= | ||
| Para poder comprobar los resultados en la escena tenemos que hallar sus centros y sus radios: | Para poder comprobar los resultados en la escena tenemos que hallar sus centros y sus radios: | ||
| {{p}} | {{p}} | ||
| - | :<math>r: \, x^2+y^2+2x=0\; \rightarrow \; \begin{cases} | + | :<math>r: \, x^2+y^2+6x+2y+1=0\; \rightarrow \; \begin{cases} |
| - | O(-\cfrac{A}{2},-\cfrac{B}{2})=(1,1) \; \rightarrow \; a=1 \, , \; b=1 | + | O(-\cfrac{A}{2},-\cfrac{B}{2})=(-3,1) |
| \\ | \\ | ||
| \\ | \\ | ||
| - | r=\sqrt{\big( \cfrac{A}{2} \big)^2+\cfrac{B}{2} \big)^2-C}=\sqrt{1^2+1^2+2}=2 | + | r=\sqrt{\big( \cfrac{A}{2} \big)^2+\cfrac{B}{2} \big)^2-C}=\sqrt{3^2+1^2-1}=3 |
| + | \end{cases}</math> | ||
| + | |||
| + | :<math>r: \, x^2+y^2-2x-4y+1=0\; \rightarrow \; \begin{cases} | ||
| + | O(-\cfrac{A}{2},-\cfrac{B}{2})=(1,2) | ||
| + | \\ | ||
| + | \\ | ||
| + | r=\sqrt{\big( \cfrac{A}{2} \big)^2+\cfrac{B}{2} \big)^2-C}=\sqrt{1^2+2^2-1}=2 | ||
| \end{cases}</math> | \end{cases}</math> | ||
| Línea 205: | Línea 215: | ||
| <center><iframe> | <center><iframe> | ||
| - | url=http://maralboran.org/web_ma/descartes/Geometria/circunferencia/circunferencia_tres_1.html | + | url=http://maralboran.org/web_ma/descartes/Geometria/circunferencia/circunferencia_tres_2.html |
| width=520 | width=520 | ||
| height=420 | height=420 | ||
| name=myframe | name=myframe | ||
| </iframe></center> | </iframe></center> | ||
| - | <center>[http://maralboran.org/web_ma/descartes/Geometria/circunferencia/circunferencia_tres_1.html '''Click''' aquí si no se ve bien la escena]</center> | + | <center>[http://maralboran.org/web_ma/descartes/Geometria/circunferencia/circunferencia_tres_2.html '''Click''' aquí si no se ve bien la escena]</center> |
| Los puntos de corte se averiguan resolviendo el sistema: | Los puntos de corte se averiguan resolviendo el sistema: | ||
| Línea 216: | Línea 226: | ||
| <center><math> | <center><math> | ||
| \begin{cases} | \begin{cases} | ||
| - | y=2x+1 | + | x^2+y^2+6x+2y+1=0 |
| \\ | \\ | ||
| - | x^2+y^2-2x-2y-2=0 | + | x^2+y^2-2x-4y+1=0 |
| \end{cases} | \end{cases} | ||
| </math></center> | </math></center> | ||
| - | Lo resolvemos por sustitución: | + | Sustituyendo la segunda ecuación por la suma de ambas, obtenemos el siguiente sistema equivalente: |
| + | |||
| + | <center><math> | ||
| + | \begin{cases} | ||
| + | x^2+y^2+6x+2y+1=0 | ||
| + | \\ | ||
| + | 4x-2y+2=0 | ||
| + | \end{cases} \; \rightarrow \; | ||
| + | \begin{cases} | ||
| + | x^2+y^2+6x+2y+1=0 | ||
| + | \\ | ||
| + | 2x-y+1=0 | ||
| + | \end{cases} \; \rightarrow \; | ||
| + | \begin{cases} | ||
| + | x^2+y^2+6x+2y+1=0 | ||
| + | \\ | ||
| + | y=2x+1 | ||
| + | \end{cases} | ||
| + | </math></center> | ||
| + | |||
| + | que resolvemos por sustitución: | ||
| - | <center><math>x^2+(2x+1)^2-2x-2(2x+1)-2=0\;</math></center> | + | <center><math>x^2+(2x+1)^2+6x+2(2x+1)+1=0\;</math></center> |
| {{p}} | {{p}} | ||
| - | <center><math>x^2+4x^2+4x+1-2x-4x-2-2=0\;</math></center> | + | <center><math>x^2+4x^2+4x+1+6x+4x+2+1=0\;</math></center> |
| {{p}} | {{p}} | ||
| - | <center><math>5x^2-2x-3=0 \; \rightarrow \; \begin{cases} | + | <center><math>5x^2+14x+4=0 \; \rightarrow \; \begin{cases} |
| x_1=1 \; \rightarrow \; y_1=3 | x_1=1 \; \rightarrow \; y_1=3 | ||
| \\ | \\ | ||
Revisión de 18:52 24 mar 2009
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
Circunferencia
La circunferencia de centro  y radio
y radio  , es el lugar geométrico de los puntos
, es el lugar geométrico de los puntos 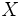 , cuya distancia al centro es
, cuya distancia al centro es  .
.
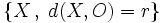
Ecuación de la circunferencia
De la anterior definición, utilizando la fórmula de la distancia entre dos puntos, tenemos:
La ecuación de la circunferencia de centro 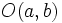 y radio
y radio  , es:
, es:
|
|
Proposición
La ecuación de una circunferencia de centro 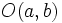 y radio
y radio  , es:
, es:
|
|
donde: 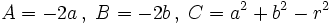 .
.
Partiendo de la ecuación de la circunferencia:

Elevando al cuadrado ambos términos:
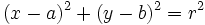
y desarrollando el radicando:
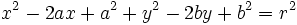
Agrupando términos:
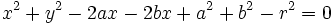
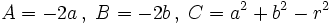 , se tiene la ecuación.
, se tiene la ecuación.Corolario
Dada la circunferencia de ecuación 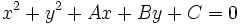 , su centro y su radio vienen dados por:
, su centro y su radio vienen dados por:
|
|
Es inmediato a partir de la proposición anterior, despejando
 ,
,  y
y  .
.|
Actividad Interactiva: Ecuación de la circunferencia
Actividad 1: En esta escena vamos a hallar la ecuación de la circunferencia de centro
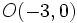 y radio y radio 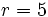 . .Actividad: Hallamos la ecuación de la cirecunferencia: 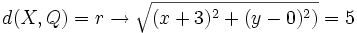 Elevando al cuadrado ambos miembros y desarrollando; 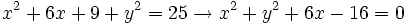
Ejercicio: Mueve el punto X a otro punto de la circunferencia y comprueba que sus coordenadas verifican su ecuación. Observa como el radio no varía. Nota: La ecuación de la circunferencia (en rojo) es editable. Prueba a cambiarla por otras ecuaciones de circunferencia para ver sus gráficas. |
Posiciones relativas de una recta y de una circunferencia
Una recta 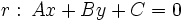 y una circunferencia
y una circunferencia 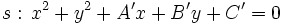 pueden ser:
pueden ser:
- Secantes: si se cortan en 2 puntos.
- Tangentes: si se cortan en un punto.
- Exteriores: si no se cortan.
Los puntos de corte se averiguan resolviendo el sistema: 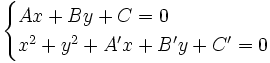
|
Actividad Interactiva: Posición relativa de recta y circunferencia
Actividad 1: En esta escena vamos a hallar la posición relativa de la recta
 y la circunferencia y la circunferencia 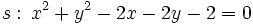 . .Actividad: Para poder comprobar los resultados en la escena, vamos a poner la ecuación de la recta en forma explícita, Y a partir de la ecuación de la circunferencia tenemos que hallar su centro y su radio, ya que la escena también nos lo exige: Su representación gráfica puedes verla en la escena:
Los puntos de corte se averiguan resolviendo el sistema: 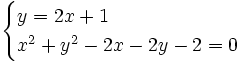 Lo resolvemos por sustitución: 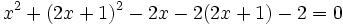 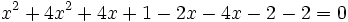 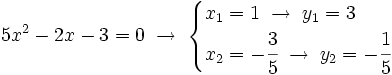 Los puntos de corte son: Ejercicio: Halla la posición relativa de la recta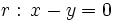 y la circunferencia y la circunferencia 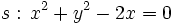 . Comprueba los resultados en la escena anterior. . Comprueba los resultados en la escena anterior. |
Posiciones relativas de dos circunferencias
Dos circunferencias pueden ser:
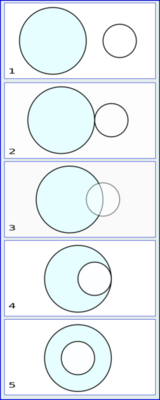
- Exteriores, si no tienen puntos comunes y la distancia que hay entre sus centros es mayor que la suma de sus radios. No importa que tengan igual o distinto radio. (Figura 1)
- Tangentes exteriormente, si tienen un punto común y todos los demás puntos de una son exteriores a la otra. La distancia que hay entre sus centros es igual a la suma de sus radios. No importa que tengan igual o distinto radio. (Figura 2)
- Secantes, si se cortan en dos puntos distintos y la distancia entre sus centros es menor a la suma de sus radios. No importa que tengan igual o distinto radio. Dos circunferencias distintas no pueden cortarse en más de dos puntos. Dos circunferencias son secantes ortogonalmente si el ángulo entre sus tangentes en los dos puntos de contacto es recto. (Figura 3)
- Tangentes interiormente, si tienen un punto común y todos los demás puntos de una de ellas son interiores a la otra exclusivamente. La distancia que hay entre sus centros es igual a la diferencia de sus radios. Una de ellas tiene que tener mayor radio que la otra. (Figura 4)
- Interiores excéntricas, si no tienen ningún punto común y la distancia entre sus centros es mayor que 0 y menor que la diferencia de sus radios. Una de ellas tiene que tener mayor radio que la otra.
- Interiores concéntricas, si tienen el mismo centro (la distancia entre sus centros es 0) y distinto radio. Forman una figura conocida como corona circular o anillo. Una de ellas tiene que tener mayor radio que la otra. (Figura 5)
- Coincidentes, si tienen el mismo centro y el mismo radio. En realidad no se trata de dos circunferencias distintas, sino de una misma. Si dos circunferencias se cortan en más de dos puntos, necesariamente son circunferencias coincidentes.
Si sus ecuaciones son:
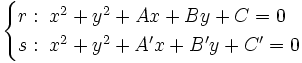
los puntos de corte se averiguan resolviendo el sistema.
|
Actividad Interactiva: Posición relativa de dos circunferencias
Actividad 1: En esta escena vamos a hallar la posición relativa de las circunferencias
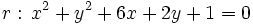 y la circunferencia y la circunferencia 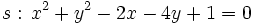 . .Actividad: Para poder comprobar los resultados en la escena tenemos que hallar sus centros y sus radios: Su representación gráfica puedes verla en la escena:
Los puntos de corte se averiguan resolviendo el sistema: 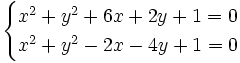 Sustituyendo la segunda ecuación por la suma de ambas, obtenemos el siguiente sistema equivalente: 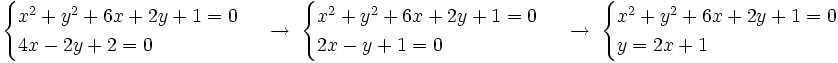 que resolvemos por sustitución: 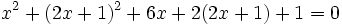 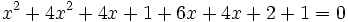 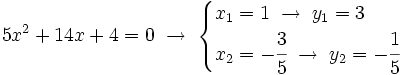 Los puntos de corte son: Ejercicio: Halla la posición relativa de la recta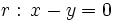 y la circunferencia y la circunferencia 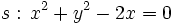 . Comprueba los resultados en la escena anterior. . Comprueba los resultados en la escena anterior. |

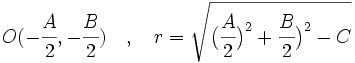
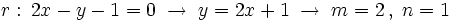
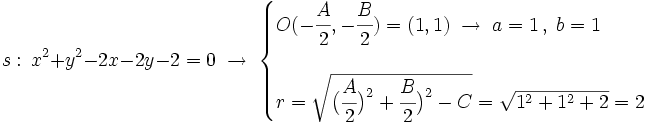
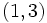 y
y