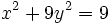La elipse (1ºBach)
De Wikipedia
| Revisión de 08:34 31 mar 2009 Coordinador (Discusión | contribuciones) (→Ecuación reducida de la elipse) ← Ir a diferencia anterior |
Revisión de 08:44 31 mar 2009 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 130: | Línea 130: | ||
| }} | }} | ||
| }} | }} | ||
| - | {{P}} | + | {{p}} |
| ==Ecuación de la elipse con los focos en el eje Y== | ==Ecuación de la elipse con los focos en el eje Y== | ||
| Línea 147: | Línea 147: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | {{AI2|titulo=Actividad interactiva: ''Ecuación reducida de la elipse''|cuerpo= | ||
| + | {{ai_cuerpo | ||
| + | |enunciado='''Actividad 1:''' En la siguiente escena vamos a calcular la ecuación de la elipse de centro O(3,-1) y semiejes 5 y 2. | ||
| + | |||
| + | |actividad=La ecuación reducida viene dada por la fórmula: | ||
| + | {{p}} | ||
| + | <center><math>\cfrac{(x-\alpha)^2}{a^2}+\cfrac{(y-\beta)^2}{b^2}=1</math></center> | ||
| + | {{p}} | ||
| + | Sustituyendo <math>a=5\,</math>, <math>b=2\,</math>, <math>\alpha=3\,</math>, <math>\beta=-1\,</math>, tenemos: | ||
| + | {{p}} | ||
| + | <center><math>\cfrac{(x-3)^2}{25}+\cfrac{(y+1)^2}{4}=1</math></center> | ||
| + | {{p}} | ||
| + | Puedes ver su gráfica en la siguente escena: | ||
| + | |||
| + | <center><iframe> | ||
| + | url=http://maralboran.org/web_ma/geogebra/figuras/elipse_3.html | ||
| + | width=780 | ||
| + | height=460 | ||
| + | name=myframe | ||
| + | </iframe></center> | ||
| + | <center>[http://maralboran.org/web_ma/geogebra/figuras/elipse_3.html '''Click''' aquí si no se ve bien la escena]</center> | ||
| + | |||
| + | '''Ejercicio:''' | ||
| + | #Usando la escena anterior, intenta representar las siguientes elipse y averigua sus parámetros. | ||
| + | {{p}} | ||
| + | :a) <math>\cfrac{(x+2)^2}{16}+\cfrac{(y-3)^2}{25}=1</math> | ||
| + | :b) <math>x^2+9y^2=9\,</math> | ||
| + | }}}} | ||
| + | {{P}} | ||
| [[Categoría: Matemáticas]][[Categoría: Geometría]] | [[Categoría: Matemáticas]][[Categoría: Geometría]] | ||
Revisión de 08:44 31 mar 2009
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
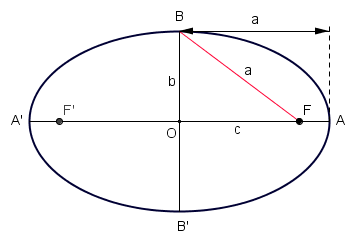
Elementos de la elipse
Una una elipse de focos
| 
|
Excentricidad de la elipse
La escentricidad de la elipse es el cociente entre la distancia focal y el eje mayor:
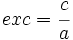
Propiedades
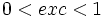 .
.
- La excentricidad mide el achatamiento de la elipse: cuanto más próxima a 1 más se parece a a una circunferencia.
- Como la hipotenusa del triángulo rectángulo es mayor que los catetos, tenemos que

- y como
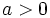 y
y  , tenemos que
, tenemos que 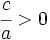
- Cuanto más próxima a 1 sea la excentricidad, más proximos son
 y
y 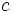 y, por tanto, más se aproxima
y, por tanto, más se aproxima  a cero.
a cero.
Ecuación reducida de la elipse
Ecuación reducida de la elipse
- La ecuación de una elipse con semieje mayor
 y semieje menor
y semieje menor  , con centro en el origen de coordenadas y focos en el eje de abscisas es:
, con centro en el origen de coordenadas y focos en el eje de abscisas es:
|
|
Sean  y
y  los focos de la elipse. Cualquier punto P(x,y) de la misma cumple:
los focos de la elipse. Cualquier punto P(x,y) de la misma cumple:
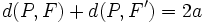
Sustituyendo las distancias por su fórmula matemática:
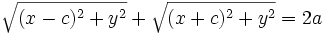
Pasamos la segunda raíz al segundo miembro:
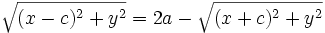
Se elevan al cuadrado ambos miebros y se simplifica:
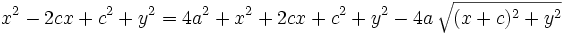
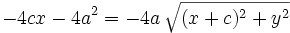
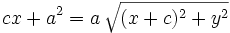
Se elevan al cuadrado los dos miembros:
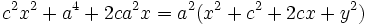
Reordenando y agrupando términos:
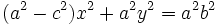
Teniendo en cuenta que 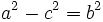 :
:
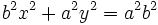
Dividiendo la expresión por 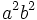 :
:
se obtiene la cuación buscada:
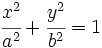
|
Actividad interactiva: Ecuación reducida de la elipse
Actividad 1: En la siguiente escena vamos a calcular la ecuación reducida de la elipse de semiejes 5 y 9.
Actividad: La ecuación reducida viene dada por la fórmula: 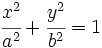 Sustituyendo a=5 y b=3, tenemos: 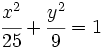 Puedes ver su gráfica en la siguente escena: Ejercicio:
|
Ecuación de la elipse con los focos en el eje Y
Ecuación de la elipse con los focos en el eje Y
- La ecuación de una elipse con semieje mayor
 y semieje menor
y semieje menor  , con centro en el origen de coordenadas y focos en el eje de ordenadas es:
, con centro en el origen de coordenadas y focos en el eje de ordenadas es:
|
|
- Su excentricidad es:
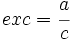
Ecuación de la elipse con el centro desplazado del origen de coordenadas
Ecuación de la elipse con el centro desplazado del origen
- La ecuación de una elipse con semiejes
 y
y  y centro
y centro 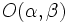 es:
es:
|
|
|
Actividad interactiva: Ecuación reducida de la elipse
Actividad 1: En la siguiente escena vamos a calcular la ecuación de la elipse de centro O(3,-1) y semiejes 5 y 2.
Actividad: La ecuación reducida viene dada por la fórmula: 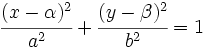 Sustituyendo  Puedes ver su gráfica en la siguente escena: Ejercicio:
|
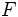 y
y 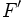 , con ejes de simetría
, con ejes de simetría 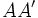 y
y 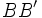 , que se cortan en el centro
, que se cortan en el centro  de la elipse, determina los siguientes segmentos:
de la elipse, determina los siguientes segmentos:
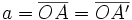
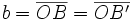
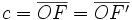
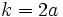 (constante de la elipse)
(constante de la elipse)
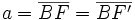
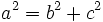
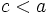
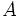 un punto de la elipse:
un punto de la elipse:
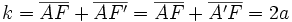
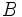 un punto de la elipse:
un punto de la elipse:
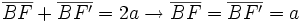
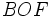 , tenemos
, tenemos

 ,
, 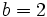 ,
, 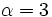 ,
,  , tenemos:
, tenemos: