La parábola (1ºBach)
De Wikipedia
| Revisión de 18:45 1 abr 2009 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 18:50 1 abr 2009 Coordinador (Discusión | contribuciones) (→Elementos de la elipse) Ir a siguiente diferencia → |
||
| Línea 48: | Línea 48: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{AI2|titulo=Actividad interactiva: ''Propiedad de la elipse''|cuerpo= | + | {{AI2|titulo=Actividad interactiva: ''Propiedad de la parábola''|cuerpo= |
| {{ai_cuerpo | {{ai_cuerpo | ||
| - | |enunciado='''Actividad 1:''' En la siguiente escena vamos a ver una propiedad de la elipse en la que veremos como cualquier "rayo de luz" que parta de uno de sus su focos (considerando que la elipse se comporta como un espejo) se refleja en la elipse y va a parar al otro foco. | + | |enunciado='''Actividad 1:''' En la siguiente escena vamos a ver una propiedad de la parábola en la que veremos como cualquier "rayo" perpendicular a la directriz que impacte en la curva se refleja y va a parar a su foco. |
| |actividad= | |actividad= | ||
| <center><iframe> | <center><iframe> | ||
| - | url=http://maralboran.org/web_ma/geogebra/figuras/elipse_5.html | + | url=http://maralboran.org/web_ma/geogebra/figuras/parabola_5.html |
| width=780 | width=780 | ||
| height=460 | height=460 | ||
| Línea 61: | Línea 61: | ||
| <center>[http://maralboran.org/web_ma/geogebra/figuras/elipse_5.html '''Click''' aquí si no se ve bien la escena]</center> | <center>[http://maralboran.org/web_ma/geogebra/figuras/elipse_5.html '''Click''' aquí si no se ve bien la escena]</center> | ||
| - | '''Ejercicios:''' | + | |
| - | *Desliza el punto verde hacia arriba. | + | '''Ejercicio:''' |
| - | **Describe lo que ves. | + | |
| - | *Utiliza el segundo deslizador para cambiar la dirección del "rayo" y repite la animación. Prueba a modificar también la forma de la elipse (arrastrando sus vértices). | + | Desliza el punto verde hacia la derecha y observa: |
| - | **¿Qué se puede decir de los rayos que salen de un foco de cualquier elipse y se reflejan en ella? | + | *Describe lo que ves. |
| - | *Arrastra el vértice derecho de la elipse hasta conseguir una circunferencia (elipse de excentricidad 0) y observa: | + | *¿Encuentra alguna relación con el funcionamiento de las antenas parabólicas? |
| - | ** ¿Qué ocurre con un rayo emitido desde el radio de una circunferencia reflejado en ella misma? | + | *¿Conoces algún otro ejemplo práctico donde se aproveche esta propiedad de la parábola? |
| - | ** ¿Qué ángulo forman el radio de una circunferencia y la tangente a la misma en el punto correspondiente? | + | |
| }} | }} | ||
| }} | }} | ||
| + | |||
| ==Construcciones de la parábola== | ==Construcciones de la parábola== | ||
| {{AI2|titulo=Actividad interactiva: ''Construcciones de la parábola''|cuerpo= | {{AI2|titulo=Actividad interactiva: ''Construcciones de la parábola''|cuerpo= | ||
Revisión de 18:50 1 abr 2009
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
La parábola
Dados un punto 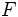 llamado foco, y una recta
llamado foco, y una recta 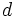 , llamada directriz, se llama parábola al lugar geométrico de los puntos
, llamada directriz, se llama parábola al lugar geométrico de los puntos  del plano que equidistán del foco y de la directriz:
del plano que equidistán del foco y de la directriz:
|
|
Elementos de la elipse
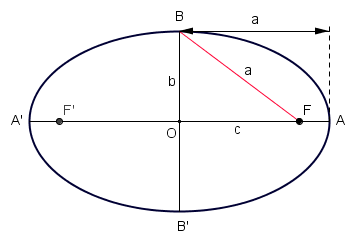
Una una elipse de focos
| 
|
|
Actividad interactiva: Propiedad de la parábola
Actividad 1: En la siguiente escena vamos a ver una propiedad de la parábola en la que veremos como cualquier "rayo" perpendicular a la directriz que impacte en la curva se refleja y va a parar a su foco.
Actividad:
Desliza el punto verde hacia la derecha y observa:
|
Construcciones de la parábola
|
Actividad interactiva: Construcciones de la parábola
Actividad 1: Método basado en su definición como lugar geométrico.
Actividad: Activa la traza, desliza el punto P y observa.
Actividad 2: La parábola como envolvente.
Actividad: Desliza el punto P y observa. Activa el trazo de la perpendicular a PF por P y vuelve a deslizar el punto P
Tras pulsar sobre para volver a la figura inicial, modifica la posición de F o de la recta directriz y repite lo anterior.
Actividad 3: La parábola generada por el centro de una circunferencia.
Actividad: Desliza el punto P y observa.
Activa el trazo del centro de la circunferencia y vuelve a deslizar el punto P.
|
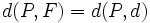
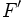 , con ejes de simetría
, con ejes de simetría 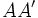 y
y 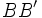 , que se cortan en el centro
, que se cortan en el centro  de la elipse, determina los siguientes segmentos:
de la elipse, determina los siguientes segmentos:
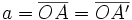
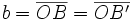
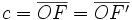
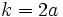 (constante de la elipse)
(constante de la elipse)
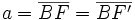
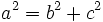
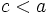
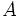 un punto de la elipse:
un punto de la elipse:
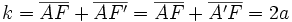
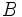 un punto de la elipse:
un punto de la elipse:
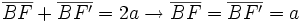
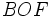 , tenemos
, tenemos
 la hipotenusa y
la hipotenusa y 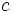 un cateto, tenemos que
un cateto, tenemos que 
