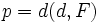La parábola (1ºBach)
De Wikipedia
| Revisión de 20:29 1 abr 2009 Coordinador (Discusión | contribuciones) (→La parábola) ← Ir a diferencia anterior |
Revisión de 20:38 1 abr 2009 Coordinador (Discusión | contribuciones) (→La parábola) Ir a siguiente diferencia → |
||
| Línea 49: | Línea 49: | ||
| Analogamente, una fuente emisora situada en el foco, enviará un haz de rayos paralelos al eje: diversas lámparas y faros tienen espejos con superficies parabólicas reflectantes para poder enviar haces de luz paralelos emanados de una fuente en posición focal. Los rayos convergen o divergen si el emisor se deplaza de la posición focal. | Analogamente, una fuente emisora situada en el foco, enviará un haz de rayos paralelos al eje: diversas lámparas y faros tienen espejos con superficies parabólicas reflectantes para poder enviar haces de luz paralelos emanados de una fuente en posición focal. Los rayos convergen o divergen si el emisor se deplaza de la posición focal. | ||
| {{Tabla4|celda1= | {{Tabla4|celda1= | ||
| - | <center>[[Imagen:Parab.gif|200px]]<br>La parábola refleja sobre el foco los rayos paralelos al eje. Analogamente, un emisor situado en el foco, enviará un haz de rayos paralelos al eje.</center> | + | <center>[[Imagen:Parab.gif|193px]] |
| + | <br>La parábola refleja sobre el foco los rayos paralelos al eje. Analogamente, un emisor situado en el foco, enviará un haz de rayos paralelos al eje.</center> | ||
| |celda2= | |celda2= | ||
| - | <center>[[Imagen:Erdfunkstelle Raisting 2.jpg|200px]]<br>Los radiotelescopios concentran los haces de señales en un receptor situado en el foco. El mismo principio se aplica en una antena de radar.</center> | + | <center>[[Imagen:Erdfunkstelle Raisting 2.jpg|165px]] |
| + | <br>Los radiotelescopios concentran los haces de señales en un receptor situado en el foco. El mismo principio se aplica en una antena de radar.</center> | ||
| |celda3= | |celda3= | ||
| - | <center>[[Imagen:Solarofen.jpg|200px]]<br>Cocina solar de concentrador parabólico. El mismo método se emplea en las grandes centrales captadoras de energía solar.</center> | + | <center>[[Imagen:Solarofen.jpg|200px]] |
| + | <br>Cocina solar de concentrador parabólico. El mismo método se emplea en las grandes centrales captadoras de energía solar.</center> | ||
| |celda4= | |celda4= | ||
| - | <center>[[Imagen:Austinlight.jpg|200px]]<br>Los faros de los automóviles envían haces de luz paralelos, si la bombilla se situa en el foco de una superficie parabólica.</center> | + | <center>[[Imagen:Austinlight.jpg|200px]] |
| + | <br>Los faros de los automóviles envían haces de luz paralelos, si la bombilla se situa en el foco de una superficie parabólica.</center> | ||
| }} | }} | ||
Revisión de 20:38 1 abr 2009
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
EN CONSTRUCCIÓN!!!!!
Tabla de contenidos |
La parábola
|
Actividad interactiva: Propiedades de la parábola
Actividad 1: En la siguiente escena vamos a ver una propiedad de la parábola en la que veremos como cualquier "rayo" perpendicular a la directriz que impacte en la curva se refleja y va a parar a su foco.
Actividad:
Aplicaciones prácticas: Una consecuencia de gran importancia es que la tangente refleja los rayos paralelos al eje de la parábola en dirección al foco. Las aplicaciones prácticas son muchas: las antenas satelitales y radiotelescopios aprovechan el principio concentrando señales recibidas desde un emisor lejano en un receptor colocado en la posición del foco. La concentración de la radiación solar en un punto, mediante un reflector parabólico tiene su aplicación en pequeñas cocinas solares y grandes centrales captadoras de energía solar. Analogamente, una fuente emisora situada en el foco, enviará un haz de rayos paralelos al eje: diversas lámparas y faros tienen espejos con superficies parabólicas reflectantes para poder enviar haces de luz paralelos emanados de una fuente en posición focal. Los rayos convergen o divergen si el emisor se deplaza de la posición focal.
Actividad 2: Tiro parabólico
Actividad:
En la figura se puede observar la trayectoria de un proyectil (cuya velocidad de salida es constante). Prueba a modificar el ángulo de inclinación inicial.
Activa el trazo de para comprobar la zona de alcance de los proyectiles.
|
Excentricidad de la parábola
La excentricidad de la parábola es el cociente entre 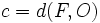 y
y 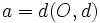 . En consecuencia, la excentricidad de la parábola es siempre igual a 1.
. En consecuencia, la excentricidad de la parábola es siempre igual a 1.
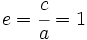
Ecuación reducida de la parábola
Ecuación reducida de la parábola
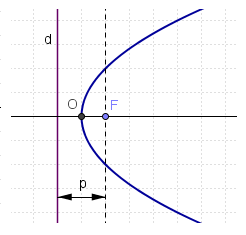
- La ecuación de una parábola con foco en el eje de abscisas, directriz paralela al eje de ordenadas y vértice en el origen de coordenadas, es:
|
|
Recordemos que 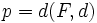 . Por tanto, las coordenadas del foco y la ecuación de la directiz son:
. Por tanto, las coordenadas del foco y la ecuación de la directiz son:
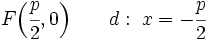
Como cualquier punto 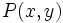 de la parábola cumple que:
de la parábola cumple que:
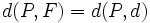
Sustituyendo las distancias por su fórmula matemática, tenemos:
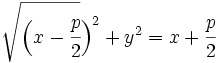
Elevando ambos miembros al cuadrado:
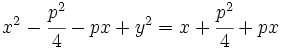
Y simplificando:
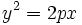
|
Actividad interactiva: Ecuación reducida de la parábola
Actividad 1: En la siguiente escena vamos a calcular la ecuación reducida de la parábola con distancia del foco a la directriz
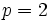 . .Actividad: La ecuación reducida viene dada por la fórmula: 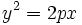 Sustituyendo 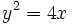 Puedes ver su gráfica en la siguente escena: Ejercicio:
|
Construcciones de la parábola
|
Actividad interactiva: Construcciones de la parábola
Actividad 1: Método basado en su definición como lugar geométrico.
Actividad: Activa la traza, desliza el punto P y observa.
Actividad 2: La parábola como envolvente.
Actividad: Desliza el punto P y observa. Activa el trazo de la perpendicular a PF por P y vuelve a deslizar el punto P
Tras pulsar sobre para volver a la figura inicial, modifica la posición de F o de la recta directriz y repite lo anterior.
Actividad 3: La parábola generada por el centro de una circunferencia.
Actividad: Desliza el punto P y observa.
Activa el trazo del centro de la circunferencia y vuelve a deslizar el punto P.
|
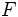 llamado foco, y una recta
llamado foco, y una recta 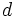 , llamada directriz, se llama parábola al lugar geométrico de los puntos
, llamada directriz, se llama parábola al lugar geométrico de los puntos  del plano que equidistán del foco y de la directriz:
del plano que equidistán del foco y de la directriz: