Plantilla:Raíces: definición y propiedades
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 12:10 23 nov 2009 Coordinador (Discusión | contribuciones) (→Raíz de un número) ← Ir a diferencia anterior |
Revisión de 12:11 23 nov 2009 Coordinador (Discusión | contribuciones) (→Raíz de un número) Ir a siguiente diferencia → |
||
| Línea 6: | Línea 6: | ||
| *Se define la '''raíz cúbica''' de un número {{sube|porcentaje=+15%|contenido=<math>a\;\!</math>}} como otro número {{sube|porcentaje=+15%|contenido=<math>b\;\!</math>}} tal que {{sube|porcentaje=+20%|contenido=<math>b^3 =a\;\!</math>}}, que escribimos simbólicamente: <math>b=\sqrt[3]{a}</math>. | *Se define la '''raíz cúbica''' de un número {{sube|porcentaje=+15%|contenido=<math>a\;\!</math>}} como otro número {{sube|porcentaje=+15%|contenido=<math>b\;\!</math>}} tal que {{sube|porcentaje=+20%|contenido=<math>b^3 =a\;\!</math>}}, que escribimos simbólicamente: <math>b=\sqrt[3]{a}</math>. | ||
| *Igualmente, se define '''raíz n-sima''' <math>(n \in \mathbb{N},\ n>1)</math>de un número {{sube|porcentaje=+15%|contenido=<math>a\;\!</math>}} como otro número {{sube|porcentaje=+15%|contenido=<math>b\;\!</math>}} tal que {{sube|porcentaje=+20%|contenido=<math>b^n =a\;\!</math>}}, que escribimos simbólicamente: <math>b=\sqrt[n]{a}</math>. | *Igualmente, se define '''raíz n-sima''' <math>(n \in \mathbb{N},\ n>1)</math>de un número {{sube|porcentaje=+15%|contenido=<math>a\;\!</math>}} como otro número {{sube|porcentaje=+15%|contenido=<math>b\;\!</math>}} tal que {{sube|porcentaje=+20%|contenido=<math>b^n =a\;\!</math>}}, que escribimos simbólicamente: <math>b=\sqrt[n]{a}</math>. | ||
| - | *El número <math>a\;\!</math> se llama '''radicando''', el número <math>n\;\!</math> '''índice''' y <math>b\;\!</math> es la '''raíz'''. | + | *El número {{sube|porcentaje=+15%|contenido=<math>a\;\!</math>}} se llama '''radicando''', el número {{sube|porcentaje=+15%|contenido=<math>n\;\!</math>}} '''índice''' y {{sube|porcentaje=+15%|contenido=<math>b\;\!</math>}} es la '''raíz'''. |
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión de 12:11 23 nov 2009
Raíz de un número
Sabemos que 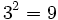 . Esta igualdad la podemos expresar de forma similar como
. Esta igualdad la podemos expresar de forma similar como 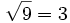 y se lee 3 es igual a la raíz cuadrada de 9.
y se lee 3 es igual a la raíz cuadrada de 9.
- Se define la raíz cuadrada de un número
 como otro número
como otro número  tal que
tal que 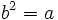 , que escribimos simbólicamente:
, que escribimos simbólicamente: 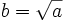 .
.
- Se define la raíz cúbica de un número
 como otro número
como otro número  tal que
tal que 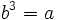 , que escribimos simbólicamente:
, que escribimos simbólicamente: ![b=\sqrt[3]{a}](/wikipedia/images/math/6/0/0/60067ca3ef9f9cd5db25de80fbfcb000.png) .
.
- Igualmente, se define raíz n-sima
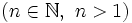 de un número
de un número  como otro número
como otro número  tal que
tal que 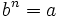 , que escribimos simbólicamente:
, que escribimos simbólicamente: ![b=\sqrt[n]{a}](/wikipedia/images/math/c/e/0/ce05f9d287d25fe0a5fd8e680bd177f5.png) .
.
- El número
 se llama radicando, el número
se llama radicando, el número  índice y
índice y  es la raíz.
es la raíz.
- Pulsa el botón "ejemplo" para ver más ejemplos de raíces cuadradas y cúbicas. Anótalos en tu cuaderno:
Propiedades de las raíces
![\sqrt[n]{1}=1](/wikipedia/images/math/f/2/3/f2301fcbef74b110ad8d373f2b32a16b.png) y
y ![\sqrt[n]{0}=0](/wikipedia/images/math/8/6/5/865db751c6cb2e12533fccdf8de1e1df.png) , para cualquier valor del índice
, para cualquier valor del índice  .
.
- Si
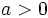 ,
, ![\sqrt[n]{a}](/wikipedia/images/math/9/a/2/9a2b6d33f3d62a1e8bd99c76f3cb79f5.png) existe cualquiera que sea el índice
existe cualquiera que sea el índice  .
.
- Si
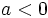 ,
, ![\sqrt[n]{a}](/wikipedia/images/math/9/a/2/9a2b6d33f3d62a1e8bd99c76f3cb79f5.png) sólo existe si el índice
sólo existe si el índice  es impar.
es impar.
- Si el índice
 es par y el radicando
es par y el radicando 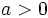 , la raíz tiene dos soluciones: una positiva y otra negativa, pero iguales en valor absoluto. Si el índice es impar, siempre tiene una única solución, que tiene el mismo signo que el radicando
, la raíz tiene dos soluciones: una positiva y otra negativa, pero iguales en valor absoluto. Si el índice es impar, siempre tiene una única solución, que tiene el mismo signo que el radicando  .
.
![\sqrt[3]{1}=1](/wikipedia/images/math/d/5/3/d53d30c7123945d21786c0fb38eeeb18.png) .
.
![\sqrt[5]{0}=0](/wikipedia/images/math/e/9/5/e95b8cee4e9e352608032036b0bd68d7.png) .
.
![\sqrt[4]{16}=\pm 2](/wikipedia/images/math/3/5/c/35cc75069a6350b569ad8c8f72bf6ae2.png) porque
porque 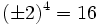 .
.
![\sqrt[3]{64}=4](/wikipedia/images/math/f/2/4/f2482a82a1ce97518a3bbef09d9575b5.png) porque
porque 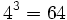 .
.
![\sqrt[3]{-8}=-2](/wikipedia/images/math/1/5/4/154ab22db729e6b6490caa36d8669830.png) porque
porque 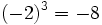 .
.
![\sqrt[4]{-8}= no \ existe](/wikipedia/images/math/a/2/1/a21d3d89fedd78f5c9a6378b3cf240f3.png) porque ningún número elevado a 4 puede dar negativo (-8).
porque ningún número elevado a 4 puede dar negativo (-8).

