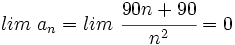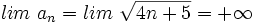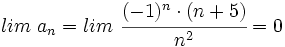Límite de una sucesión (1ºBach)
De Wikipedia
| Revisión de 16:57 27 sep 2014 Coordinador (Discusión | contribuciones) (→Videotutoriales sobre límite de sucesiones) ← Ir a diferencia anterior |
Revisión de 17:04 27 sep 2014 Coordinador (Discusión | contribuciones) (→Videotutoriales sobre límite de sucesiones) Ir a siguiente diferencia → |
||
| Línea 208: | Línea 208: | ||
| |duracion=10´35" | |duracion=10´35" | ||
| |url1=http://matematicasbachiller.com/videos/universidad/sucesiones-y-series/01-sucesiones/0301-ejercicio-3#.VCbrTPl_u2E | |url1=http://matematicasbachiller.com/videos/universidad/sucesiones-y-series/01-sucesiones/0301-ejercicio-3#.VCbrTPl_u2E | ||
| + | |sinopsis=Videotutorial | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Video_enlace2 | ||
| + | |titulo1=Límites infinitos | ||
| + | |duracion=21´27" | ||
| + | |url1=http://matematicasbachiller.com/videos/universidad/sucesiones-y-series/01-sucesiones/04-limites-infinitos#.VCbsn_l_u2E | ||
| + | |sinopsis=Videotutorial | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Video_enlace2 | ||
| + | |titulo1=Propiedades aritméticas de los límites | ||
| + | |duracion=14´20" | ||
| + | |url1=http://matematicasbachiller.com/videos/universidad/sucesiones-y-series/01-sucesiones/05-propiedades-aritmeticas-de-los-limites#.VCbs1fl_u2E | ||
| + | |sinopsis=Videotutorial | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Video_enlace2 | ||
| + | |titulo1=Indeterminaciones matemáticas | ||
| + | |duracion=8´10" | ||
| + | |url1=http://matematicasbachiller.com/videos/universidad/sucesiones-y-series/01-sucesiones/06-indeterminaciones-matematicas#.VCbtBfl_u2E | ||
| + | |sinopsis=Videotutorial | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Video_enlace2 | ||
| + | |titulo1=Infinitos potenciales | ||
| + | |duracion=6´54" | ||
| + | |url1=http://matematicasbachiller.com/videos/universidad/sucesiones-y-series/01-sucesiones/07-infinitos-potenciales#.VCbtP_l_u2E | ||
| + | |sinopsis=Videotutorial | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Video_enlace2 | ||
| + | |titulo1=Cociente de infinitos potenciales | ||
| + | |duracion=9´09" | ||
| + | |url1=http://matematicasbachiller.com/videos/universidad/sucesiones-y-series/01-sucesiones/08-cociente-de-infinitos-potenciales#.VCbtaPl_u2E | ||
| + | |sinopsis=Videotutorial | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Video_enlace2 | ||
| + | |titulo1=Otros infinitos | ||
| + | |duracion=13´01" | ||
| + | |url1=http://matematicasbachiller.com/videos/universidad/sucesiones-y-series/01-sucesiones/09-otros-infinitos#.VCbtqPl_u2E | ||
| |sinopsis=Videotutorial | |sinopsis=Videotutorial | ||
| }} | }} | ||
| [[Categoría: Matemáticas]][[Categoría: Números]] | [[Categoría: Matemáticas]][[Categoría: Números]] | ||
Revisión de 17:04 27 sep 2014
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Para acercarnos a la idea de límite, vamos a empezar viendo algunas representaciones gráficas de sucesiones
Tabla de contenidos |
Representación gráfica de una sucesión
Para representar gráficamente una sucesión  , construiremos una tabla donde anotaremos el valor de
, construiremos una tabla donde anotaremos el valor de  para valores distintos valores de n.
para valores distintos valores de n.
Las parejas 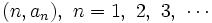 obtenidas en la tabla, son las coordenadas de los puntos de la representación gráfica de la sucesión, que dibujaremos en unos ejes de coordenadas cartesianos.
obtenidas en la tabla, son las coordenadas de los puntos de la representación gráfica de la sucesión, que dibujaremos en unos ejes de coordenadas cartesianos.
Ejemplos: Representación gráfica de una sucesión
Representa graficamente las siguientes sucesiones:
- a)

- b)

- a)
a) 
Construimos la tabla de valores:
Se observa que los términos de la sucesión se acercan cada vez mas a 0. Concluiremos diciendo que el límite de esta sucesión es 0, y lo escribiremos simbólicamente de la siguiente manera: 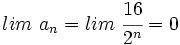 |
b) 
Construimos la tabla de valores:
Se observa que los términos crecen y se hacen indefinidamente grandes. Concluiremos diciendo que el límite de esta sucesión es  |
Aproximación a la idea de límite de una sucesión
- Cuando los términos de una sucesión
 se aproximan a un número
se aproximan a un número 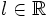 , decimos que dicha sucesión tiende a
, decimos que dicha sucesión tiende a 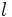 o que su límite es
o que su límite es 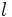 . Lo escribiremos simbólicamente:
. Lo escribiremos simbólicamente:
 o bien
o bien 
- Cuando los términos de una sucesión
 crecen indefinidamente, superando a cualquier número, decimos que dicha sucesión tiende a
crecen indefinidamente, superando a cualquier número, decimos que dicha sucesión tiende a 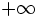 o que su límite es
o que su límite es 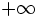 . Lo escribiremos simbólicamente:
. Lo escribiremos simbólicamente:
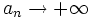 o bien
o bien 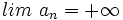
- Cuando los términos de una sucesión
 decrecen indefinidamente, tomando valores infriores a cuialquier número negativo, decimos que dicha sucesión tiende a
decrecen indefinidamente, tomando valores infriores a cuialquier número negativo, decimos que dicha sucesión tiende a 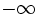 o que su límite es
o que su límite es 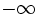 . Lo escribiremos simbólicamente:
. Lo escribiremos simbólicamente:
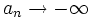 o bien
o bien 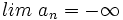
Sucesiones que no tienen límite
Hay sucesiones que no cumplen ninguna de las tres condiciones expuestas en el apartado anterior. Dichas sucesiones diremos que no tienen límite.
Ejemplo: Sucesión sin límite
La siguiente sucesión no tiene límite
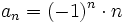
En efecto, los términos de esta sucesión son:
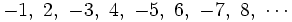
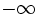 y los pares a
y los pares a 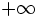
Ejercicios
|
Ejercicio: Límite de una sucesión
Solución: Límites:
Representación gráfica: En la siguiente escena tienes la representación gráfica de las sucesiones. Pulsa los cursores "sucesión" para cambiar de sucesión. Haz uso del zoom y del cambio de escala O.x y O.y para visualizar mejor los resultados. Mueve el punto amarillo para ver la sucesión término a término. |
Videotutoriales sobre límite de sucesiones
Videotutorial
Videotutorial
- Definición rigurosa de límite de una sucesión de números reales.
- Ejemplos
- Visualización del concepto de límite
Videotutorial
Videotutorial
Videotutorial
Videotutorial
Videotutorial
Videotutorial
Videotutorial
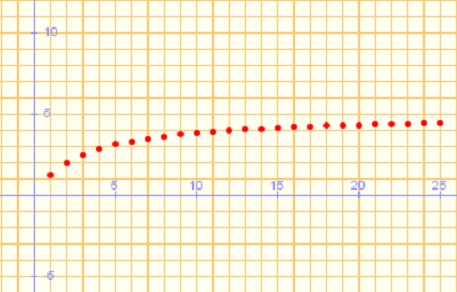
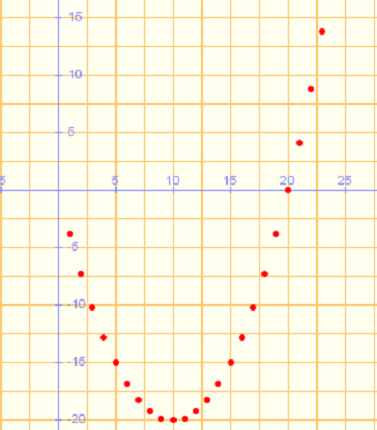
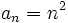
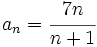
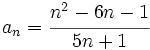
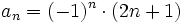

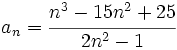



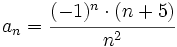
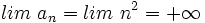
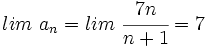
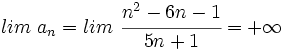
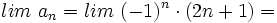 (No tiene límite) Es oscilante
(No tiene límite) Es oscilante