Plantilla:Máximo común divisor
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 19:25 7 oct 2014 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 19:35 7 oct 2014 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 20: | Línea 20: | ||
| Dos números son '''primos entre sí''', si su m.c.d. es 1.}}{{p}} | Dos números son '''primos entre sí''', si su m.c.d. es 1.}}{{p}} | ||
| Por ejemplo, 6 y 11 son primos entre sí. | Por ejemplo, 6 y 11 son primos entre sí. | ||
| + | |||
| + | {{wolfram | ||
| + | |titulo=Actividad: ''Máximo común divisor'' | ||
| + | |cuerpo= | ||
| + | {{ejercicio_cuerpo | ||
| + | |enunciado= | ||
| + | |||
| + | :a) Halla el m.c.d.(30,150,700) | ||
| + | |||
| + | {{p}} | ||
| + | |sol= | ||
| + | Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones: | ||
| + | |||
| + | :a) {{consulta|texto=gcd(30, 150, 700)}} | ||
| + | |||
| + | {{widget generico}} | ||
| + | }} | ||
| + | }} | ||
Revisión de 19:35 7 oct 2014
El máximo común divisor (m.c.d.) de dos o más números es el mayor de todos los divisores comunes a esos números.
Para obtenerlo se descomponen los números en factores primos y se toman los factores comunes elevados al menor exponente.
Ejemplo: m.c.d.
- Calcula el m.c.d.(24,60).
Solución:
Descomponemos 24 y 60 en sus factores primos:
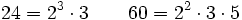
Multiplicando los factores comunes elevados al menor exponente:
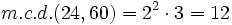
Propiedad
Si a es múltiplo de b, entonces m.c.d.(a,b)=b.
Por ejemplo, m.c.d.(15, 30)=15.
Números primos entre sí
Dos números son primos entre sí, si su m.c.d. es 1.
Por ejemplo, 6 y 11 son primos entre sí.
|
Actividad: Máximo común divisor
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|

