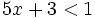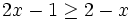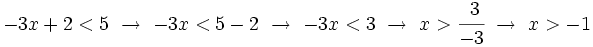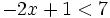Plantilla:Inecuaciones lineales con una incógnita
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 12:25 12 oct 2014 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 09:53 16 ago 2016 Coordinador (Discusión | contribuciones) (→Método gráfico de resolución) Ir a siguiente diferencia → |
||
| Línea 27: | Línea 27: | ||
| {{p}} | {{p}} | ||
| {{Ejemplo|titulo=Ejemplo: ''Inecuaciones lineales con una incógnita'' | {{Ejemplo|titulo=Ejemplo: ''Inecuaciones lineales con una incógnita'' | ||
| - | |enunciado=Resuelve la siguiente inecuación por el método gráfico: | + | |enunciado=:Resuelve la siguiente inecuación por el método gráfico: |
| <center><math>2x-3 \le 0 \;</math></center> | <center><math>2x-3 \le 0 \;</math></center> | ||
| |sol= | |sol= | ||
| Línea 48: | Línea 48: | ||
| |enunciado= | |enunciado= | ||
| - | Resuelve: | + | :Resuelve: |
| - | :a) <math>-2x+1<7\,</math> | + | ::<math>-2x+1<7\,</math> |
| {{p}} | {{p}} | ||
Revisión de 09:53 16 ago 2016
- Una inecuación lineal con una incógnita es una inecuación que puede ponerse de alguna de estas formas:
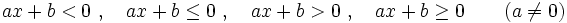
Ejemplos:
Son inecuaciones lineales con una incógnita:
Método algebraico de resolución
El método algebraico aplica las anteriores transformaciones para conseguir dejar despejada la incógnita.
Ejemplo: Inecuaciones lineales con una incógnita
Resuelve la siguiente inecuación:
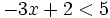
Solución:
- Solución:
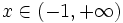
Método gráfico de resolución
El método gráfico requiere que el miembro de la derecha de la inecuación sea cero, lo cual puede conseguirse mediante las transformaciones antes mencionadas.
Ejemplo: Inecuaciones lineales con una incógnita
- Resuelve la siguiente inecuación por el método gráfico:
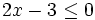
Solución:
Representamos la recta 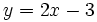 y nos fijamos para que valores de x, la gráfica está por debajo del eje X (es negativa) o vale cero.
y nos fijamos para que valores de x, la gráfica está por debajo del eje X (es negativa) o vale cero.
![x \in (- \infty, 1.5])](/wikipedia/images/math/6/c/9/6c98ec58684ed6f35d05405a20cba0d9.png)
|
Actividad: Inecuaciones lineales con una incógnita
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|