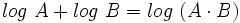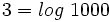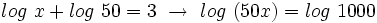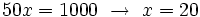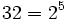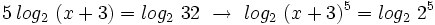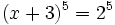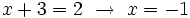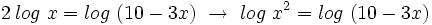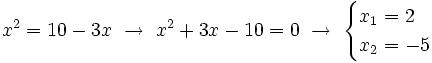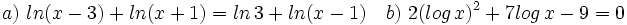Plantilla:Ecuaciones logaritmicas
De Wikipedia
| Revisión de 17:56 29 ago 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 17:58 29 ago 2016 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 29: | Línea 29: | ||
| :<math>50x=1000 \ \rightarrow \ x=20</math> | :<math>50x=1000 \ \rightarrow \ x=20</math> | ||
| + | |||
| + | Se comprueba en la ecuación de partida y resulta ser válida. | ||
| <br> | <br> | ||
| '''''Solución:''''' <math>x=20\;</math> | '''''Solución:''''' <math>x=20\;</math> | ||
| Línea 50: | Línea 52: | ||
| :<math>x+3= 2 \ \rightarrow \ x=-1</math> | :<math>x+3= 2 \ \rightarrow \ x=-1</math> | ||
| + | Se comprueba en la ecuación de partida y resulta ser válida. | ||
| '''''Solución:''''' <math>x=-1\;</math> | '''''Solución:''''' <math>x=-1\;</math> | ||
| Línea 63: | Línea 66: | ||
| :<math>x^2= 10-3x \ \rightarrow \ x^2+3x-10=0 \ \rightarrow \ \begin{cases} x_1=2 \\ x_2=-5 \end{cases}</math> | :<math>x^2= 10-3x \ \rightarrow \ x^2+3x-10=0 \ \rightarrow \ \begin{cases} x_1=2 \\ x_2=-5 \end{cases}</math> | ||
| - | De las dos soluciones, <math>x_2=-5\;</math> no es válida, porque al comprobarla en la ecuación de partida, <math>log x\;</math> no se puede calcular para <math>x=-5\;</math> (El logaritmo de un número negativo no existe). | + | De las dos soluciones, <math>x_2=-5\;</math> no es válida, porque al comprobarla en la ecuación de partida, <math>log \ x\;</math> no se puede calcular para <math>x=-5\;</math> (El logaritmo de un número negativo no existe). |
| - | + | <br> | |
| - | + | ||
| '''''Solución:''''' <math>x=2\;</math> | '''''Solución:''''' <math>x=2\;</math> | ||
Revisión de 17:58 29 ago 2016
Las ecuaciones logarítmicas son aquellas en las que la incógnita aparece como parte de un logaritmo.
Para su resolución hay que tener en cuenta las propiedades de los logaritmos.
Se deben comprobar siempre las soluciones en la ecuación de partida pues pueden obtenerse soluciones que no sean válidas, como puede verse en el ejemplo c) siguiente.
Ejemplos: Ecuaciones logarítmicas
Resuelve las siguientes ecuaciónes:
- a)
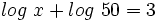
- a)
- b)
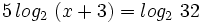
- b)
- c)
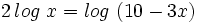
- c)
a) 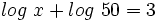
Teniendo en cuenta que:
tenemos:
Y teniendo en cuenta que 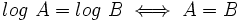 , se tiene:
, se tiene:
Se comprueba en la ecuación de partida y resulta ser válida.
Solución: 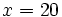
b) 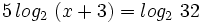
Teniendo en cuenta que:
tenemos:
Como 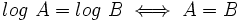 , se tiene:
, se tiene:
Y, como 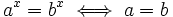
Se comprueba en la ecuación de partida y resulta ser válida.
Solución: 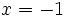
c) 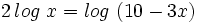
Teniendo en cuenta que 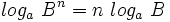 , tenemos:
, tenemos:
Como 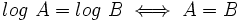 , se tiene:
, se tiene:
De las dos soluciones, 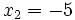 no es válida, porque al comprobarla en la ecuación de partida,
no es válida, porque al comprobarla en la ecuación de partida, 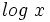 no se puede calcular para
no se puede calcular para 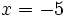 (El logaritmo de un número negativo no existe).
(El logaritmo de un número negativo no existe).

Videotutoriales sobre ecuaciones logarítmicas
Videotutorial
Videotutorial
Videotutorial
Videotutorial
|
Actividad: Ecuaciones logarítmicas Resuelve las siguientes ecuaciones: Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
Nota: En WolframAlpha log y loge simbolizan el logaritmo neperiano mientras que el logaritmo decimal es log10. |