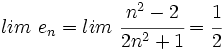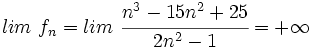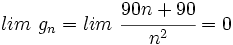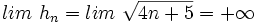Límite de una sucesión (1ºBach)
De Wikipedia
| Revisión de 19:19 1 sep 2016 Coordinador (Discusión | contribuciones) (→Ejercicios) ← Ir a diferencia anterior |
Revisión de 19:28 1 sep 2016 Coordinador (Discusión | contribuciones) (→Ejercicios) Ir a siguiente diferencia → |
||
| Línea 175: | Línea 175: | ||
| ===Ejercicios=== | ===Ejercicios=== | ||
| - | (pág. 59) | ||
| {{p}} | {{p}} | ||
| {{Ejemplo|titulo=Ejercicios resueltos: ''Aproximación a la idea de límite de una sucesión'' | {{Ejemplo|titulo=Ejercicios resueltos: ''Aproximación a la idea de límite de una sucesión'' | ||
| Línea 222: | Línea 221: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | (pág. 63) | ||
| {{ejercicio | {{ejercicio | ||
| |titulo=Ejercicios propuestos: ''Aproximación a la idea de límite de una sucesión'' | |titulo=Ejercicios propuestos: ''Aproximación a la idea de límite de una sucesión'' | ||
| Línea 235: | Línea 235: | ||
| {{b4}}{{b4}}c) <math>c_n=3-2^n \;</math> | {{b4}}{{b4}}c) <math>c_n=3-2^n \;</math> | ||
| - | {{b4}}{{b4}}d) <math>c_n=5- \frac{1}{n^3} \;</math> | + | {{b4}}{{b4}}d) <math>d_n=5- \frac{1}{n^3} \;</math> |
| <br> | <br> | ||
| Línea 244: | Línea 244: | ||
| {{b4}}{{b4}}b) <math>b_n=(-1)^n \cdot \frac{n}{n+4}</math> | {{b4}}{{b4}}b) <math>b_n=(-1)^n \cdot \frac{n}{n+4}</math> | ||
| - | {{b4}}{{b4}}c) <math>c_n=(-1)^n \cdot n</math> | + | {{b4}}{{b4}}c) <math>c_n=(-1)^n \cdot n^2</math> |
| - | {{b4}}{{b4}}d) <math>c_n=(-1)^n \cdot \frac{2}{n^2}</math> | + | {{b4}}{{b4}}d) <math>d_n=(-1)^n \cdot \frac{2}{n^2}</math> |
| {{p}} | {{p}} | ||
| |sol=Utiliza Wolfram para comprobar las soluciones. | |sol=Utiliza Wolfram para comprobar las soluciones. | ||
Revisión de 19:28 1 sep 2016
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Para acercarnos a la idea de límite, vamos a empezar viendo algunas representaciones gráficas de sucesiones
Tabla de contenidos |
Representación gráfica de una sucesión
(pág. 61)
Para representar gráficamente una sucesión  , construiremos una tabla donde anotaremos el valor de
, construiremos una tabla donde anotaremos el valor de  para distintos valores de n.
para distintos valores de n.
Las parejas 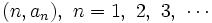 obtenidas en la tabla, son las coordenadas de los puntos de la representación gráfica de la sucesión, que dibujaremos en unos ejes de coordenadas cartesianos.
obtenidas en la tabla, son las coordenadas de los puntos de la representación gráfica de la sucesión, que dibujaremos en unos ejes de coordenadas cartesianos.
Ejercicios resueltos: Representación gráfica de una sucesión
- Representa graficamente las siguientes sucesiones:
- a)
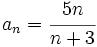
- a)
- b)

- b)
a) 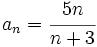
Construimos la tabla de valores:
Se observa que los términos de la sucesión se acercan cada vez mas a 5. Concluiremos diciendo que el límite de esta sucesión es 0, y lo escribiremos simbólicamente de la siguiente manera: 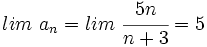 |
b) 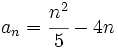
Construimos la tabla de valores:
Se observa que los términos crecen y se hacen indefinidamente grandes. Concluiremos diciendo que el límite de esta sucesión es 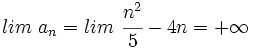 |
Observa que, en ambos ejemplos, los valores obtenidos cuando n es pequeño, no son representativos del valor del límite. Por tanto, el valor del límite debe deducirse tomando valores de n suficientemente grandes.
Ejercicios
|
Actividad: Representación gráfica y límite de una sucesión 1. Dada la sucesión
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones: 1.
2.
|
(pág. 61)
|
Ejercicios propuestos: Límite de una sucesión |
Aproximación a la idea de límite de una sucesión
(pág. 58)
- Cuando los términos de una sucesión
 se aproximan a un número
se aproximan a un número 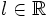 , decimos que dicha sucesión tiende a
, decimos que dicha sucesión tiende a 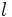 o que su límite es
o que su límite es 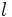 . Diremos que la sucesión es convergente. Lo escribiremos simbólicamente:
. Diremos que la sucesión es convergente. Lo escribiremos simbólicamente:

- Cuando los términos de una sucesión
 superan a cualquier número "k" tan grande como queramos, al darle a "n" valores suficientemente grandes, decimos que dicha sucesión tiende a
superan a cualquier número "k" tan grande como queramos, al darle a "n" valores suficientemente grandes, decimos que dicha sucesión tiende a 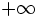 o que su límite es
o que su límite es 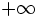 . Diremos que la sucesión es divergente. Lo escribiremos simbólicamente:
. Diremos que la sucesión es divergente. Lo escribiremos simbólicamente:
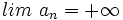
- Cuando los términos de una sucesión
 toman valores inferiores a cualquier número "k" negativo tan pequeño como queramos, al darle a "n" valores suficientemente grandes, decimos que dicha sucesión tiende a
toman valores inferiores a cualquier número "k" negativo tan pequeño como queramos, al darle a "n" valores suficientemente grandes, decimos que dicha sucesión tiende a 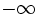 o que su límite es
o que su límite es 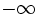 . Diremos que la sucesión es divergente. Lo escribiremos simbólicamente:
. Diremos que la sucesión es divergente. Lo escribiremos simbólicamente:
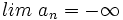
Sucesiones que no tienen límite
(pág. 58)
Hay sucesiones que no cumplen ninguna de las tres condiciones expuestas en el apartado anterior. Dichas sucesiones diremos que no tienen límite.
Ejemplo: Sucesión oscilante
- La siguiente sucesión no tiene límite
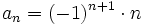
| En efecto, los términos de esta sucesión son:
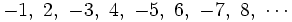
Esto es debido a que sus términos se aproximan a dos valores distintos: los términos impares tienden a |
Ejercicios
Ejercicios resueltos: Aproximación a la idea de límite de una sucesión
- 1. Estudiar el comportamiento de las siguientes sucesiones para valores de n avanzados e indicar su límite:
- a)
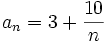
- a)
- b)
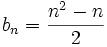
- b)
- 2. Comprobar si las siguientes sucesiones tienen límite:
- a)
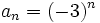
- a)
- b)
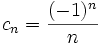
- b)
Utilizaremos Wolfram para comprobarlos:
- 1a.
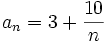
- Table[3+10/n,{n,1.,10.}] o Table[3+10/n,{n,1.,1000.,100}]
- Plot Table[3+10/n,{n,1.,1000.,100}]
- limit 3+10/n as n->+oo
- 1b.
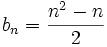
- Table[(n^2-n)/2,{n,1.,10.}] o Table[(n^2-n)/2,{n,1.,1000.,100}]
- Plot Table[(n^2-n)/2,{n,1.,1000.,100}]
- limit (n^2-n)/2 as n->+oo
- 2a.
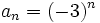
- Table[(-3)^n,{n,1.,10.}] o Table[(-3)^n,{n,1.,1000.,100}]
- Plot Table[(-3)^n,{n,1.,1000.,100}]
- limit (-3)^n as n->+oo
- 2b.
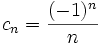
- Table[(-1)^n/n,{n,1.,10.}] o Table[(-1)^n/n,{n,1.,1000.,100}]
- Plot Table[(-1)^n/n,{n,1.,1000.,100}]
- limit (-1)^n/n as n->+oo
(pág. 63)
|
Ejercicios propuestos: Aproximación a la idea de límite de una sucesión |
Ejercicios
|
Ejercicio: Límite de una sucesión
Solución: Límites:
Representación gráfica: En la siguiente escena tienes la representación gráfica de las sucesiones. Pulsa los cursores "sucesión" para cambiar de sucesión. Haz uso del zoom y del cambio de escala O.x y O.y para visualizar mejor los resultados. Mueve el punto amarillo para ver la sucesión término a término. |
Videotutoriales (Ampliación)
- Concepto de sucesión de números reales. Ejemplos.
- Introducción de la notación necesaria para el comprender el concepto de límite de una sucesión de números reales.
- Representación gráfica de una sucesión de números reales.
- Definición rigurosa de límite finito de una sucesión de números reales. (sucesión convergente)
- Ejemplos.
- Visualización del concepto de límite.
- Demostrar que
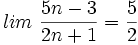 usando la definición rigurosa de límite.
usando la definición rigurosa de límite.
- Definición rigurosa de límite infinito (sucesión divergente)
- Ejemplos.
- Visualización del concepto de límite infinito.
- Propiedades aritméticas de los límites (límite de una suma, de un producto, de un cociente, de una potencia, etc.)
- Ejemplos.
- Indeterminaciones matemáticas.
- Las diversas indeterminaciones matemáticas.
- Definición de infinito potencial de grado k.
- Ejemplos.
- Cociente de infinitos potenciales.
- Ejemplos.
- Definición de infinito de orden superior, inferior o igual a otro infinito.
- Ejemplos.
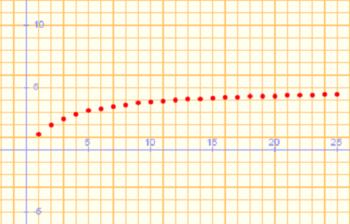
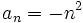
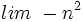
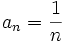
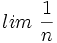
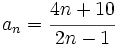 y asígnale un valor a su límite.
y asígnale un valor a su límite.
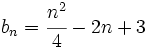 y asígnale un valor a su límite.
y asígnale un valor a su límite.
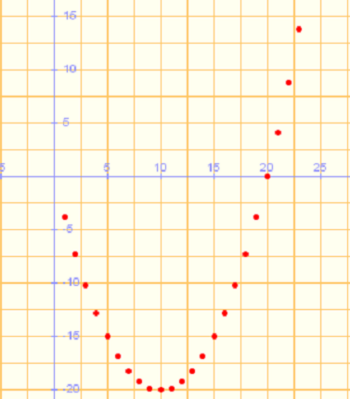
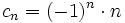 y describe su comportamiento. ¿Qué puede decirse sobre
y describe su comportamiento. ¿Qué puede decirse sobre 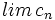 ?
?
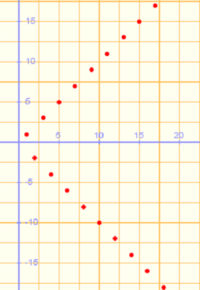
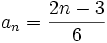
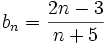
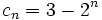
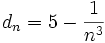
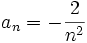
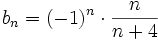
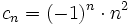
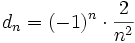
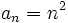
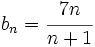
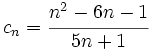
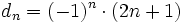
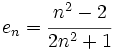
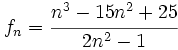
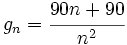
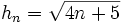
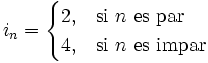
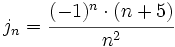
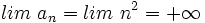
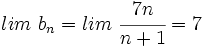
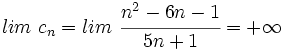
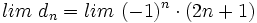 (No tiene límite, es oscilante)
(No tiene límite, es oscilante)