Números naturales (3ºESO Aplicadas)
De Wikipedia
Revisión de 06:26 6 sep 2016
| Enlaces internos | Para repasar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra |
(pág. 11-13)
Tabla de contenidos |
Números naturales
El conjunto de los números naturales es:
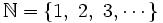
Se trata de un conjunto con infinitos elementos y sirven para:
- Contar (números cardinales: 1, 2, 3, ...).
- Ordenar (números ordinales: 1º, 2º, 3º, ...).
- Identificar y diferenciar los distintos elementos de un conjunto.
Puesto que los números naturales se utilizan para contar elementos, el cero (0) puede considerarse el número que corresponde a la ausencia de los mismos. Dependiendo del área de las matemáticas, el conjunto de los números naturales puede incluir o no al cero.
Veamos distintos ejemplos de uso de los números naturales:
- Como número cardinal: Los días de la semana son 7.
- Como número ordinal: El atleta británico quedó 3º en la prueba de cien metros lisos.
- Como identificador: Tú número de carnet de socio del Atleti es el 2868.
El conjunto de los números naturales: origen y definición.
El conjunto de los números naturales: origen y definición.
Tutorial de introducción al tema:
- Números naturales.
- Sistemas de numeración.
- Sistema de numeración decimal.
Hace unas horas tenía 16 años y el año que viene cumpliré 19. ¿Cómo explicas esta situación?
Ejercicios de autoevaluación sobre números naturales.
Existen dos teorías sobre el origen de la numeración, que además está relacionada con la cuestión de qué números aparecieron primero, los cardinales (1, 2, 3,...) o los ordinales (1º, 2º, 3º,...) La teoría que genera más consenso defiende el argumento de la necesidad. Todo habría comenzado a causa de la necesidad de contar objetos; por ello se habrían creado primero los números cardinales y después, los ordinales.
La otra teoría defiende la base espiritual de los números, que habrían tenido un uso ritual: cierto tipo de ceremonias requerían que los participantes se desplazaran o se situaran en un orden ritual preestablecido; por eso los números ordinales serían anteriores a los cardinales. Esta teoría además postula que los números se originaron en un lugar geográfico determinado, desde el que se propagaron al resto del mundo; también establece la división de los números naturales en pares e impares, considerando los impares masculinos y los pares, femeninos, una clasificación que comparten hoy en día muchas culturas del planeta.
(Extracto de "El mundo es matemático: Del ábaco a la revolución industrial". Pág. 10)"
Véanse los artículos de la BBC:
- ¿Sabes que el 1 y el 2 no son del mismo género y que los números tienen personalidades?
- Lo que quizás no sabías de los números
|
Ejercicios propuestos: Números naturales |
Fracciones equivalentes
Plantilla:Fracciones equivalentes
Simplificación de fracciones
- Simplificar una fracción es sustituirla por otra equivalente con el numerador y denominador menores que los de partida.
- Cuando una fracción no se puede simplificar se dice que es irreducible.
Procedimiento: Simplificación
- Para simplificar fracciones se divide numerador y denominador por un mismo número, distinto de 0 y 1. Este proceso se puede repetir hasta hacer la fracción irreducible.
- Si queremos hacer la fracción irreducible en un solo paso debemos dividir numerador y denominador por el m.c.d. de ambos.
Simplifica 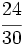 :
:
Solución:
- Paso a paso: Dividimos por 2 y luego por 3
- En un solo paso: Calculamos el m.c.d.(24,30) = 6, y dividimos directamente por 6:
Simplificación de fracciones (3 métodos). Fracción irreducible. Ejemplos.
Simplifica:
Simplifica:
Simplifica:
Simplifica:
Simplifica:
Simplifica:
Simplifica: Simplifica: Simplifica: Simplifica: Simplifica: Simplifica: | Simplifica: Simplifica: Halla la fracción irreducible de: Halla la fracción irreducible de: Halla la fracción irreducible de: Halla la fracción irreducible de: Halla la fracción irreducible de: Halla la fracción irreducible de: Halla la fracción irreducible de: Halla la fracción irreducible de: Halla la fracción irreducible de: Halla la fracción irreducible de: |
- Actividades en las que deberás simplificar fracciones con o sin ayuda.
- Actividad en la que debes emparejar cada fracción con su irreducible.
Actividad en las que deberás encontrar la fracción irreducible.
Actividades de nivel variable en las que deberás simplificar fracciones.
Simplifica fracciones.
La simplificación de fracciones me proporciona un método para saber si dos fracciones son equivalentes.
Procedimiento
Si al simplificar dos fracciones se obtiene la misma fracción irreducible, entonces las dos fracciones son equivalentes.
Determina si 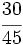 y No se pudo entender (función desconocida\cfrc): \cfrc{54}{81}
y No se pudo entender (función desconocida\cfrc): \cfrc{54}{81}
son fracciones equivalentes.
Ordenación de fracciones
Una forma de comparar fracciones consistía en calcular su valor numérico, efectuando la división. A continuación vamos a ver otras formas distintas de hacerlo. Distinguiremos los siguientes casos:
Caso 1: Las fracciones tienen numeradores o denominadores iguales
En algunos casos es fácil comparar dos fracciones sin necesidad de hacer la división. Esto será posible si ambas fracciones tienen los numeradores o denominadores iguales.
Comparar fracciones con numeradores o denominadores iguales
- De dos fracciones con el mismo denominador, es mayor la de mayor numerador.
- De dos fracciones con el mismo numerador, es mayor la de menor denominador.
Comparando fracciones con mismo denominador o mismo numerador.
Compara fracciones con el mismo numerador o denominador.
Caso 2: Las fracciones tienen numeradores y denominadores distintos
Veamos ahora un procedimiento para los casos en que no sean iguales ni los numeradores ni los denominadores. Lo que haremos será reducirlas a común denominador.
En la animación anterior, cuando los denominadores son distintos, no podemos comparar las piezas coloreadas de verde, pues son de tamaños distintos. Al cambiar los denominadores por 12, sí podemos hacer la comparación. Además, 12 no es un denominador cualquiera, es el mínimo común múltiplo de 3 y 4. Se podría usar cualquier otro múltiplo común, pero lo normal es usar el menor posible para no trabajar con números muy grandes.
Ordenar fracciones
- Para ordenar fracciones con distinto denominador debemos primero reducirlas a común denominador.
- Una vez reducidas a común denominador, será mayor la de mayor numerador.
Ejemplo: Ordenar fracciones
Ordena las siguientes fracciones: 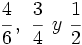
Calculamos el m.c.m. de los denominadores:
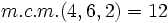 .
.
A continuación, las reducimos a común denominador:
Nótese que hemos multiplicado numerador y denominador por el resultado de dividir el m.c.m. , 12, por cada denominador.
Ordenamos las fracciones obtenidas, y a partir de ellas las fracciones de partida:
Ordena las siguientes fracciones:
a) 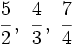
b) 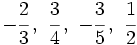
b) 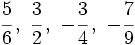
Comparación de fracciones. Ordenar fracciones de forma ascendente. Atención al método usado para obtener el m.c.m. Ordenar fracciones de forma descendente. Compara Compara Compara | Compara Compara Compara Compara las fracciones: Ordena las fracciones: Ordena las fracciones: |
Actividad en la que podrás ver como se comparan fracciones reduciéndolas a común denominador, tanto si son positivas como negativas.
Actividad en la que debes ordenas varias fracciones.
Actividad en la deberás comparar fracciones.
Ejercicios de autoevaluación sobre ordenación y comparación de fracciones.
Ordena fracciones.
Ejercicio resuelto: Ordenación de fracciones
- Ordena las fracciones:

- Repasar:
|
Actividad: Fracciones equivalentes
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
|
Actividad: Simplicar fracciones
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
|
Actividad: Ordenar fracciones
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
|
Ejercicios propuestos: Ordenación de fracciones |
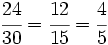
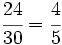
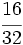 b)
b) 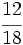
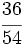 b)
b) 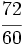
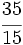 b)
b) 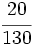
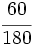 b)
b) 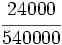
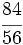 b)
b) 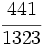
 b)
b) 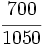
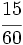
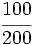 .
.
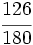 .
.
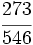 .
.
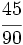 .
.
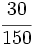 .
.
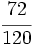 .
.
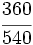 .
.
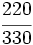 .
.
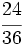 .
.
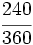 .
.
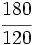 .
.
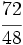 .
.
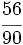 .
.
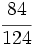 .
.
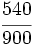 .
.
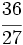 .
.
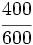 .
.
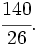
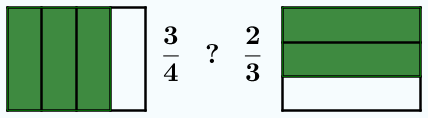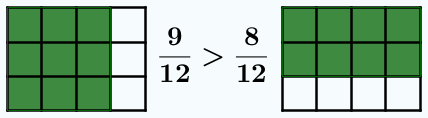
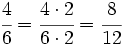
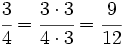
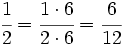
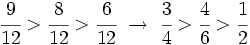
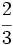 y
y 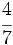 mediante la comparación de los productos cruzados.
mediante la comparación de los productos cruzados.
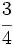 y
y 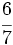 mediante la comparación de los productos cruzados.
mediante la comparación de los productos cruzados.
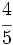 y
y 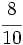 mediante la comparación de los productos cruzados.
mediante la comparación de los productos cruzados.
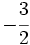 y
y 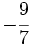 mediante la comparación de los productos cruzados.
mediante la comparación de los productos cruzados.
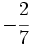 y
y 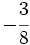 mediante la comparación de los productos cruzados.
mediante la comparación de los productos cruzados.
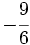 y
y 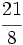 y
y 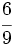 .
.
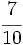 ,
, 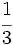 y
y 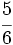 .
.
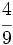 ,
, 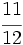 y
y 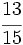 .
.
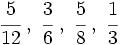
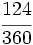 y
y 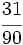 ?
?

