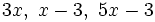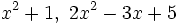Plantilla:Divisibilidad de polinomios
De Wikipedia
| Revisión de 16:42 9 sep 2016 Coordinador (Discusión | contribuciones) (→Polinomios múltiplos y divisores) ← Ir a diferencia anterior |
Revisión de 16:44 9 sep 2016 Coordinador (Discusión | contribuciones) (→Polinomios múltiplos y divisores) Ir a siguiente diferencia → |
||
| Línea 14: | Línea 14: | ||
| <center><math> P(x)=(3x^3-14x^2+4x+3) \, , \quad Q(x)=(3x+1) \, , \quad C(x)=x^2-5x+3</math>:</center> | <center><math> P(x)=(3x^3-14x^2+4x+3) \, , \quad Q(x)=(3x+1) \, , \quad C(x)=x^2-5x+3</math>:</center> | ||
| {{p}} | {{p}} | ||
| - | <math>Q(x)|P(x)\;</math>, porque <math>P(x)=\,Q(x)\cdot C(x)\,</math>. | + | Se cumple que |
| + | {{p}} | ||
| + | <center><math>Q(x)|P(x)\;</math>, porque <math>P(x)=\,Q(x)\cdot C(x)\,</math>.</center> | ||
| {{p}} | {{p}} | ||
| Es decir, la siguiente división es exacta: | Es decir, la siguiente división es exacta: | ||
| Línea 20: | Línea 22: | ||
| <center><math> (3x^3-14x^2+4x+3):(3x+1)=x^2-5x+3\;</math></center> | <center><math> (3x^3-14x^2+4x+3):(3x+1)=x^2-5x+3\;</math></center> | ||
| {{p}} | {{p}} | ||
| - | o equivalentemente: | + | porque: |
| {{p}} | {{p}} | ||
| <center><math>(3x+1) \cdot (x^2-5x+3) =3x^3-14x^2+4x+3</math></center> | <center><math>(3x+1) \cdot (x^2-5x+3) =3x^3-14x^2+4x+3</math></center> | ||
Revisión de 16:44 9 sep 2016
Polinomios múltiplos y divisores
Un polinomio 
es divisor de otro, 
y lo representaremos por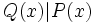 
, si la división 
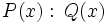es exacta, es decir, cuando existe otro polinomio 
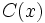tal que:
|
|
También diremos que es divisible por o que es un múltiplo de .
Dados los polinomios:
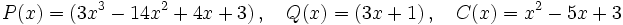:Se cumple que
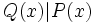, porque 
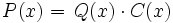.Es decir, la siguiente división es exacta:
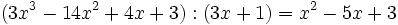
porque:
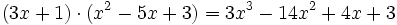
La divisibilidad de polinomios es semejante a la divisibilidad con números enteros. Asimismo, la factorización de polinomios equivale a la descomposición de un número en factores primos, y los conceptos de máximo común divisor, mínimo común múltiplo e irreducibilidad son similares a los correspondientes conceptos numéricos.
Polinomios irreducibles
Un polinomio es irreducible cuando ningún polinomio de grado inferior es divisor suyo.
Son polinomios irreducibles, entre otros:
- Los de primer grado:
- Los de segundo grado sin raíces:
