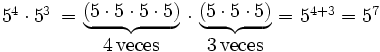Operaciones con potencias (1ºESO)

De Wikipedia

(Diferencia entre revisiones)

Revisión de 10:09 11 sep 2016

Menú:

Enlaces internos	Para repasar	Para ampliar	Enlaces externos
Indice Descartes Manual Casio			WIRIS Geogebra Calculadora

Tabla de contenidos

1 Propiedades de las potencias
2 Ejercicios propuestos

(Pág. 31)

Propiedades de las potencias

Propiedades de las potencias

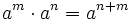
1. Producto de potencias de la misma base: $a^m \cdot a^n=a^{n+m}$

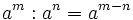
2. Cociente de potencias de la misma base: $a^m : a^n=a^{m-n}\,\!$

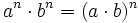
3. Potencia de un producto: $a^n \cdot b^n=(a \cdot b)^n$

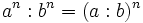
4. Potencia de un cociente: $a^n : b^n=(a : b)^n\,\!$

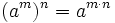
5. Potencia de otra potencia: $(a^m)^n=a^{m \cdot n}$

Ejemplos:

Producto de potencias de la misma base:

$\begin{matrix} 5^4 \cdot 5^3 \, \\ \; \end{matrix} \begin{matrix} \ = \ \\ \; \end{matrix} \begin{matrix} \underbrace{ (5 \cdot 5 \cdot 5 \cdot 5) } \\ 4 \, \mbox{veces} \end{matrix} \begin{matrix} \ \cdot \ \\ \; \end{matrix} \begin{matrix} \underbrace{ (5 \cdot 5 \cdot 5) } \\ 3 \, \mbox{veces} \end{matrix} \begin{matrix} \ = \ \\ \; \end{matrix} \begin{matrix} 5^{4+3} = 5^7 \\ \; \end{matrix}$

Potencia de un producto:

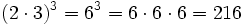
$(2 \cdot 3)^3 = 6^3 = 6 \cdot 6 \cdot 6 = 216$

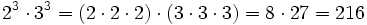
$2^3 \cdot 3^3 = (2 \cdot 2 \cdot 2) \cdot (3 \cdot 3 \cdot 3) = 8 \cdot 27 = 216$

Las dos formas de hacerlo son equivalentes.

Potencia de un cociente:

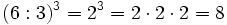
$(6 : 3)^3 = 2^3 = 2 \cdot 2 \cdot 2 = 8$

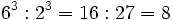
$6^3 : 2^3 = 16 : 27 = 8\;$

Las dos formas de hacerlo son equivalentes.

Potencia de otra potencia:

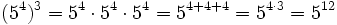
$(5^4)^3 = 5^4 \cdot 5^4 \cdot 5^4 = 5^{4+4+4} = 5^{4 \cdot 3} = 5^{12}$

Potencia cero: Cuando se vio la definición de potencia, dijimos que 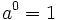$a^0 = 1\;$ por convenio. Expliquemos ésto ahora un poco mejor:

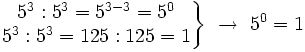
$\left.\begin{matrix} 5^3:5^3 =5^{3-3}=5^0 \\ 5^3:5^3=125:125=1 \end{matrix}\right\} \ \rightarrow \ 5^0 = 1$

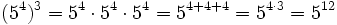
$(5^4)^3 = 5^4 \cdot 5^4 \cdot 5^4 = 5^{4+4+4} = 5^{4 \cdot 3} = 5^{12}$

Propiedades de las potencias

1. Producto de potencias de la misma base

Actividad:

Para ver paso a paso las transformaciones debes pulsar sobre el triángulo azul de arriba de la escena.

El producto de varias potencias de la misma base equivale a otra potencia cuya base es la misma y cuyo exponente es la suma de los exponentes.

Click aquí si no se ve bien la escena

2. Cociente de potencias de la misma base

Actividad:

Para ver paso a paso las transformaciones debes pulsar sobre el triángulo azul de arriba de la escena.

El cociente de dos potencias de la misma base equivale a otra potencia cuya base es la misma y cuyo exponente es la resta de los exponentes.

Click aquí si no se ve bien la escena

3. Potencia de una potencia

Actividad:

Para ver paso a paso las transformaciones debes pulsar sobre el triángulo azul de arriba de la escena.

La potencia de una potencia equivale a una potencia simple cuya base es la misma y cuyo exponente es el producto de los exponentes.

Click aquí si no se ve bien la escena

4. Potencia de un producto

Actividad:

Para ver paso a paso las transformaciones debes pulsar sobre el triángulo azul de arriba de la escena.

La potencia de un producto equivale al producto de potencias cuyas bases son cada uno de los factores y cuyo exponente es el mismo.

Click aquí si no se ve bien la escena

(Pág. 31-32)

Ejercicios resueltos: Operaciones con potencias

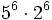
a) Calcula por el camino más sencillo: $5^6 \cdot 2^6\;$

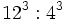
b) Calcula por el camino más sencillo: $12^3 : 4^3\;$

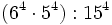
c) Calcula con la ayuda de las propiedades: $(6^4 \cdot 5^4):15^4\;$

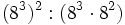
d) Calcula con la ayuda de las propiedades: $(8^3)^2 :(8^3 \cdot 8^2)\;$

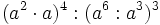
e) Reduce a una sola potencia: $(a^2 \cdot a)^4 :(a^6:a^3)^3\;$

Solución:

a) Aplicando la propiedad 3:

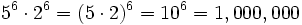
$5^6 \cdot 2^6 = (5 \cdot 2)^6 = 10^6 = 1,000,000$

b) Aplicando la propiedad 4:

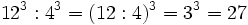
$12^3 : 4^3 = (12 : 4)^3 = 3^3 = 27\;$

c) Aplicando la propiedad 3:

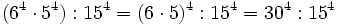
$(6^4 \cdot 5^4):15^4 = (6 \cdot 5)^4 : 15^4 = 30^4 : 15^4$

y aplicando la propiedad 4:

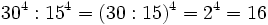
$30^4 : 15^4 = (30 : 15)^4 = 2^4 =16\;$

d) Aplicando las propiedades 5 y 1:

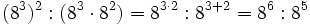
$(8^3)^2 :(8^3 \cdot 8^2) = 8^{3 \cdot 2} : 8^{3+2} = 8^6 : 8^5$

y aplicando la propiedad 2:

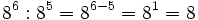
$8^6 : 8^5 = 8^{6-5} = 8^1 = 8\;$

e) Por las propiedades 1 y 2:

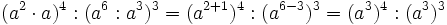
$(a^2 \cdot a)^4 :(a^6:a^3)^3= (a^{2+1})^4 : (a^{6-3})^3 =(a^3)^4 : (a^3)^3$

y por las propiedades 5 y 2:

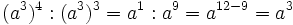
$(a^3)^4 : (a^3)^3 = a^1 : a^9 = a^{12-9} = a^3\;$

Ejercicios propuestos

Ejercicios propuestos: Operaciones con potencias

(Pág. 33)

3; 6a,c,e; 7a,d; 8a,d; 9; 10

1; 2; 4; 5; 6b,d,f; 7b,c,e,f; 8b,c,e,f

Obtenido de "http://maralboran.org/wikipedia/index.php/Operaciones_con_potencias_%281%C2%BAESO%29"

Categorías: Matemáticas | Números

 {{p}}
 *'''Potencia de otra potencia:'''
+{{p}}
+<center><math>(5^4)^3 = 5^4 \cdot 5^4 \cdot 5^4 = 5^{4+4+4} = 5^{4 \cdot 3} = 5^{12}</math></center>
+*'''Potencia cero:''' Cuando se vio la definición de potencia, dijimos que <math>a^0 = 1\;</math> por convenio. Expliquemos ésto ahora un poco mejor:
+<math>\left.\begin{matrix}
+^3:5^3 =5^{3-3}=5^0
+\\
+^3:5^3=125:125=1
+\end{matrix}\right\} \ \rightarrow \ 5^0 = 1</math>
 {{p}}
 <center><math>(5^4)^3 = 5^4 \cdot 5^4 \cdot 5^4 = 5^{4+4+4} = 5^{4 \cdot 3} = 5^{12}</math></center>

Operaciones con potencias (1ºESO)

De Wikipedia

Revisión de 10:09 11 sep 2016

Tabla de contenidos

Propiedades de las potencias

Ejercicios propuestos

Vistas

Herramientas personales

Menú

Buscar

Herramientas