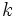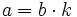Plantilla:Relacion de divisibilidad
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 19:10 11 sep 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 19:12 11 sep 2016 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 1: | Línea 1: | ||
| + | ==Relación de divisibilidad== | ||
| {{Caja_Amarilla|texto= | {{Caja_Amarilla|texto= | ||
| Dos números ''a'' y ''b'' están emparentados por la '''relación de divisibilidad''' cuando la división a:b es exacta. | Dos números ''a'' y ''b'' están emparentados por la '''relación de divisibilidad''' cuando la división a:b es exacta. | ||
| Línea 8: | Línea 9: | ||
| *Un listón de 60 cm no se puede partir, exactamente, en trozos de 25 cm, porque la división 60:25 no es exacta (cociente=2; resto=10). Así, 60 y 25 no están emparentados por la relación de divisibilidad. | *Un listón de 60 cm no se puede partir, exactamente, en trozos de 25 cm, porque la división 60:25 no es exacta (cociente=2; resto=10). Así, 60 y 25 no están emparentados por la relación de divisibilidad. | ||
| }} | }} | ||
| + | {{p}} | ||
| + | ==Multiplo y divisor== | ||
| + | {{Caja_Amarilla|texto=Si <math>a\;</math> y {{Sube|porcentaje=+10%|contenido=<math>b\;</math>}} <math>(a > b)\;</math> están emparentados por la relación de divisibilidad ({{Sube|porcentaje=+20%|contenido=<math>a : b\;</math>}} es exacta), entonces decimos que: | ||
| + | |||
| + | *{{Sube|porcentaje=+10%|contenido=<math>a\;</math>}} es '''multiplo''' {{Sube|porcentaje=+15%|contenido=<math>b\;</math>}} y lo expresaremos simbólicamente: {{Sube|porcentaje=+30%|contenido=<math>a= \dot b</math>}}. | ||
| + | *{{Sube|porcentaje=+15%|contenido=<math>b\;</math>}} es '''divisor''' de {{Sube|porcentaje=+10%|contenido=<math>a\;</math>}} y lo expresaremos simbólicamente: <math>b|a \;\!</math>. | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Ejemplo_simple|titulo=Ejemplos:|contenido= | ||
| + | *La división 60:15=4 es exacta. Entonces 60 es un múltiplo de 15 {{Sube|porcentaje=+15%|contenido=<math>(60= \dot 15)</math>}} y 15 es un divisor de 60 {{Sube|porcentaje=+15%|contenido=<math>(15|60 \;\!)</math>}}. | ||
| + | *Fíjate que 4 también es divisor de 60 porque la división 60:4=15 es también exacta. Por tanto, los divisores siempre van por parejas. | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Teorema|titulo=Proposición|enunciado= | ||
| + | :Si {{Sube|porcentaje=+10%|contenido=<math>a\;\!</math>}} es multiplo de {{Sube|porcentaje=+15%|contenido=<math>b\,</math>}} , entonces existe un número natural {{Sube|porcentaje=+15%|contenido=<math>k\;\!</math>}} tal que {{Sube|porcentaje=+20%|contenido=<math>a=b \cdot k</math>}}. | ||
| + | |demo=En efecto, si ''a'' es multiplo de ''b'', entonces la división ''a:b'' es exacta. Si llamamos ''k'' al cociente, se cumple que {{Sube|porcentaje=+20%|contenido=<math>a=b \cdot k</math>}}.}} | ||
| + | {{p}} | ||
Revisión de 19:12 11 sep 2016
Relación de divisibilidad
Dos números a y b están emparentados por la relación de divisibilidad cuando la división a:b es exacta.
- Un listón de 60 cm se puede partir, exactamente, en trozos de 15 cm, porque la división 60:15 es exacta (cociente=4; resto=0). Por tanto, 60 y 15 están emparentados por la relación de divisibilidad.
- Un listón de 60 cm no se puede partir, exactamente, en trozos de 25 cm, porque la división 60:25 no es exacta (cociente=2; resto=10). Así, 60 y 25 no están emparentados por la relación de divisibilidad.
Multiplo y divisor
Si  y
y 
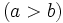 están emparentados por la relación de divisibilidad (
están emparentados por la relación de divisibilidad (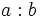 es exacta), entonces decimos que:
es exacta), entonces decimos que:
 es multiplo
es multiplo  y lo expresaremos simbólicamente:
y lo expresaremos simbólicamente: 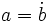 .
.
 es divisor de
es divisor de  y lo expresaremos simbólicamente:
y lo expresaremos simbólicamente: 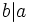 .
.
- La división 60:15=4 es exacta. Entonces 60 es un múltiplo de 15
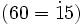 y 15 es un divisor de 60
y 15 es un divisor de 60 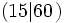 .
.
- Fíjate que 4 también es divisor de 60 porque la división 60:4=15 es también exacta. Por tanto, los divisores siempre van por parejas.