Plantilla:Descomposición factorial de un número
De Wikipedia
| Revisión de 07:51 6 sep 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 07:29 12 sep 2016 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 49: | Línea 49: | ||
| :90:9=10. Obtenemos 9 y 10. | :90:9=10. Obtenemos 9 y 10. | ||
| Paramos porque el siguiente divisor es 10, que ya se ha obtenido. | Paramos porque el siguiente divisor es 10, que ya se ha obtenido. | ||
| - | }}{{p}} | ||
| - | {{AI2|titulo=Actividad Interactiva: ''Divisores de un número''|cuerpo= | ||
| - | {{ai_cuerpo | ||
| - | |enunciado=1. Calcula los divisores de un número. | ||
| - | |actividad= | ||
| - | Marca el número que quieras en la ventana del control que está bajo la escena y pulsa intro, así aparecerán todos los divisores que tiene ese número. | ||
| - | |||
| - | También puedes ir variando el valor del número utilizando los triángulos arriba y abajo. | ||
| - | El número más grande que puedes marcar es el 10.000 | ||
| - | |||
| - | <center><iframe> | ||
| - | url=http://maralboran.org/web_ma/descartes/1y2_eso/Multiplos_divisores/divisores_1.html | ||
| - | width=420 | ||
| - | height=420 | ||
| - | name=myframe | ||
| - | </iframe></center> | ||
| - | <center>[http://maralboran.org/web_ma/descartes/1y2_eso/Multiplos_divisores/divisores_1.html '''Click''' aquí si no se ve bien la escena]</center> | ||
| - | Investiga y contesta en tu cuaderno: | ||
| - | |||
| - | Toma nota de la cantidad de divisores de cada uno de los números del 0 al 50 | ||
| - | :a) ¿Cuál es el número natural que tiene mayor cantidad de divisores? ¿Cuántos divisores tiene? | ||
| - | :b) ¿Cuál es el número natural que tiene menor cantidad de divisores? ¿Cuántos divisores tiene? | ||
| - | :c) ¿Cuántos divisores tiene un número primo? | ||
| - | Marca un número de 4 cifras, pulsa intro, con el triángulo arriba vete aumentando de uno en uno el valor del número. Observa la disparidad de número de divisores que tiene cada número. Anota lo que observes. | ||
| - | :d) ¿Crees que un número grande es de esperar necesariamente que tenga más divisores? | ||
| - | :e) ¿De qué crees que depende? | ||
| - | |||
| - | }} | ||
| - | }} | ||
| - | <br> | ||
| - | {{wolfram | ||
| - | |titulo=Actividad: ''Divisores de un número'' | ||
| - | |cuerpo= | ||
| - | {{ejercicio_cuerpo | ||
| - | |enunciado= | ||
| - | |||
| - | :a) Halla los divisores de 156 | ||
| - | |||
| - | {{p}} | ||
| - | |sol= | ||
| - | Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones: | ||
| - | |||
| - | :a) {{consulta|texto=divisors 156}} | ||
| - | |||
| - | {{widget generico}} | ||
| - | }} | ||
| - | |||
| }} | }} | ||
Revisión de 07:29 12 sep 2016
Se le llama descomposición factorial o factorización de un número, a su expresión como producto de potencias de números primos.
Descomposición en factores primos
Cualquier número puede expresarse como producto de potencias de números primos.
El procedimiento es el siguiente:
- Lo dividimos por el menor número primo que podamos.
- El cociente que haya resultado lo colocamos debajo del número.
- Si podemos, seguimos dividiendo sucesivamente ese cociente por el mismo número primo.
- Cuando no podamos hacer la división por ese número primo, lo hacemos por el siguiente primo que se pueda.
- Así sucesivamente hasta que el cociente final sea 1.
- El producto de todos los números primos por los que hemos ido dividiendo constituyen la descomposición factorial del número.
Halla la descomposición factorial de 90.
Solución:
Dividimos 90 entre el primer número primo por el que sea divisible. En este caso, por 2. (90:2=45) A continuación, procedemos a dividir 45, cociente de la anterior división, de igual forma. (45:3=15) Así sucesivamente hasta obtener 1 en el cociente (15:3=5; 5:5=1)
Los cocientes 2, 3, 3 y 5 son los factores que descomponen a 90.
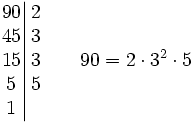
|
Actividad Interactiva: Descomposición factorial de un número
1. Descompón un número en factores primos.
Actividad: Esta escena realiza la descomposición factorial de un número, para ello marca el número natural que quieras en la ventana del control que está bajo la escena y pulsa intro. El número más grande que puedes marcar es de cinco cifras. A la derecha puedes ver los factores que intervienen y abajo la expresión del producto de potencias. Si el exponente es 1 no se pone exponente. Realiza en tu cuaderno y comprueba en la escena anterior la descomposición en factores de los números: a) 700 b) 1024 c) 658 |
|
Actividad: Descomposición factorial de un número Descompón en factores primos el número 156 Solución: Para averiguar la solución debes escribir donde pone "Escribe tu consulta" la siguiente expresión: factor 156 |
Obtención de los divisores de un número
Para obtener los divisores de un número podemos proceder siguiendo uno de los dos métodos que ilustramos con el siguiente ejemplo:
Ejemplo: Obtener los divisores de un número
- Obtén los divisores de 90.
Método 1: Descomponemos 90 en factores primos:
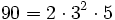
Construimos una tabla para formar las posibles combinaciones de productos de factores.
Cada casilla de la tabla contiene un divisor: 1, 3, 9, 2, 6, 18, 5, 15, 45, 10, 30 y 90.
Método 2: Dividimos 90 por su primer divisor:
- 90:1=90. Ya tenemos dos divisores: 1 y 90.
Dividimos 90 por el siguiente divisor:
- 90:2=45. Ya tenemos otros dos: 2 y 45.
Proseguimos de igual forma:
- 90:3=30. Obtenemos 3 y 30.
- 90:5=18. Obtenemos 5 y 18.
- 90:6=15. Obtenemos 6 y 15.
- 90:9=10. Obtenemos 9 y 10.