Ampliación del concepto de ángulo (1ºBach)
De Wikipedia
| Revisión de 18:43 15 sep 2016 Coordinador (Discusión | contribuciones) (→Videotutoriales) ← Ir a diferencia anterior |
Revisión de 18:45 15 sep 2016 Coordinador (Discusión | contribuciones) (→Ángulos negativos) Ir a siguiente diferencia → |
||
| Línea 62: | Línea 62: | ||
| |sinopsis=Un ángulo se dice "orientado" si uno de sus lados se bautiza "lado origen" y el otro lado se bautiza "lado extremo". | |sinopsis=Un ángulo se dice "orientado" si uno de sus lados se bautiza "lado origen" y el otro lado se bautiza "lado extremo". | ||
| Si para hacer coincidir el lado origen con el lado extremo se gira alrededor del vértice en sentido contrario a las agujas del reloj, el ángulo se dice "positivo" o "levógiro", diciéndose "negativo" o "dextrógiro" si se gira en el sentido a las agujas del reloj. | Si para hacer coincidir el lado origen con el lado extremo se gira alrededor del vértice en sentido contrario a las agujas del reloj, el ángulo se dice "positivo" o "levógiro", diciéndose "negativo" o "dextrógiro" si se gira en el sentido a las agujas del reloj. | ||
| - | |||
| - | }} | ||
| - | {{p}} | ||
| - | {{Video_enlace | ||
| - | |titulo1=Reducción de un ángulo al primer giro | ||
| - | |duracion=7´03" | ||
| - | |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/06-angulos-orientados/02-reduccion-de-un-angulo-al-primer-giro#.VChL8RZ8HA8 | ||
| - | |sinopsis=Si un ángulo orientado "A" tiene medida superior a 360º, del único ángulo orientado "B" con medida inferior a 360º cuyos lados coinciden con los de "A" se dice "reducción al primer giro" de "A". | ||
| }} | }} | ||
Revisión de 18:45 15 sep 2016
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Ángulos coterminales
Dos ángulos  y
y 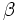 son coterminales (
son coterminales (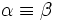 ), si se diferencian en un número entero de vueltas a la circunferencia goniométrica. Es decir,
), si se diferencian en un número entero de vueltas a la circunferencia goniométrica. Es decir,
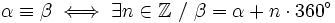 .
.Los ángulos coterminales, al tener la misma posición dentro de la circunferencia goniométrica, van a tener las mismas razones trigonométricas.
- Los ángulos 30º, 390º (30º+360º) y 750º (30º+2·360º) son coterminales.
- 3000º es coterminal con 120º porque la división 3000:360 da 120 de resto.
Ángulos negativos
Los ángulos positivos son aquellos que siguen el sentido contrario de las agujas del reloj en la circunferencia goniométrica. Los ángulos negativos, por el contrario, siguen el sentido de las agujas del reloj.
Proposición
Dado un ángulo negativo, existe un ángulo positivo coterminal con él. En consecuencia, las razones trigonométricas de ángulos negativos, las podemos estudiar sobre ángulos positivos coterminales con él.
Es inmediato, dado un ángulo negativo, basta sumarle 360º un número suficiente de veces, para obtener un ángulo positivo coterminal con él.
Como los ángulos coterminales ocupan la misma posición en la circunferencia goniométrica, sus razones trigonométricas serán las mismas.- El ángulo -60º tiene por coterminal al ángulo 300º (-60º+360º). Por tanto, las razones trigonométricas de -60º y 300º son las mismas.
|
Actividad: Ángulos coterminales
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Un ángulo se dice "orientado" si uno de sus lados se bautiza "lado origen" y el otro lado se bautiza "lado extremo". Si para hacer coincidir el lado origen con el lado extremo se gira alrededor del vértice en sentido contrario a las agujas del reloj, el ángulo se dice "positivo" o "levógiro", diciéndose "negativo" o "dextrógiro" si se gira en el sentido a las agujas del reloj.
Ejercicios propuestos
|
Ejercicios propuestos: Angulos coterminales |

