Razones trigonométricas de ángulos cualesquiera (1ºBach)
De Wikipedia
| Revisión de 09:40 17 sep 2016 Coordinador (Discusión | contribuciones) (→Signo de las razones trigonométricas) ← Ir a diferencia anterior |
Revisión de 09:50 17 sep 2016 Coordinador (Discusión | contribuciones) (→Signo de las razones trigonométricas) Ir a siguiente diferencia → |
||
| Línea 73: | Línea 73: | ||
| |descripcion=En esta escena podrás ver como se representan las razones trigonométricas de un ángulo de cualquier cuadrante. | |descripcion=En esta escena podrás ver como se representan las razones trigonométricas de un ángulo de cualquier cuadrante. | ||
| |enlace=[https://ggbm.at/mfj4NVXn Razones trigonométricas de un ángulo cualquiera] | |enlace=[https://ggbm.at/mfj4NVXn Razones trigonométricas de un ángulo cualquiera] | ||
| + | }} | ||
| + | |||
| + | {{p}} | ||
| + | {{Geogebra_enlace | ||
| + | |descripcion=En esta escena podrás ver los valores y el signo de las 6 razones trigonométricas de un ángulo de cualquier cuadrante. | ||
| + | |enlace=[https://ggbm.at/QT4AaGjP Valores y signo de razones trigonométricas de un ángulo cualquiera] | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión de 09:50 17 sep 2016
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
(Pág. 107)
Circunferencia goniométrica
Vamos a establecer un sistema de referencia para el estudio de los ángulos de cualquier cuadrante.
Consideremos una circunferencia de radio 1 centrada en un sistema de referencia cartesiano, es decir, con su centro en el origen de coordenadas O. Sobre ella situaremos nuestro triángulo rectángulo ABC, haciendo coincidir su vértice A con O, el cateto contiguo al ángulo  lo situaremos en el eje X positivo y la hipotenusa coincidiendo con el radio, tal y como se muestra en la figura. A esta circunferencia la llamaremos circunferencia goniométrica.
lo situaremos en el eje X positivo y la hipotenusa coincidiendo con el radio, tal y como se muestra en la figura. A esta circunferencia la llamaremos circunferencia goniométrica.
Teniendo en cuenta que 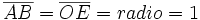 , las razones trigonométricas del águlo , las razones trigonométricas del águlo  se expresan de la siguiente manera: se expresan de la siguiente manera:
|
Videotutorial.
Razones trigonométricas de un ángulo cualquiera
Obsérvese como las coordenadas del punto B, del apartado anterior, son 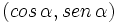 . Así podemos dar la siguiente definición del seno y del coseno de un ángulo de cualquier cuadrante:
. Así podemos dar la siguiente definición del seno y del coseno de un ángulo de cualquier cuadrante:
- Dado un ángulo
 , se define el coseno y el seno de dicho ángulo, como las coordenadas del punto de corte, B, del segundo lado del ángulo con la circunferencia goniométrica:
, se define el coseno y el seno de dicho ángulo, como las coordenadas del punto de corte, B, del segundo lado del ángulo con la circunferencia goniométrica:
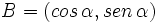
- Definiremos la tangente del ángulo, como:
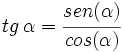 ,
, 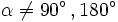
Signo de las razones trigonométricas
Los ejes cartesianos dividen a la circunferencia goniométrica en cuatro regiones denominadas cuadrantes:
- Un ángulo
 , pertenece al primer cuadrante si
, pertenece al primer cuadrante si 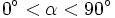
- Un ángulo
 , pertenece al segundo cuadrante si
, pertenece al segundo cuadrante si 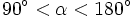
- Un ángulo
 , pertenece al tercer cuadrante si
, pertenece al tercer cuadrante si 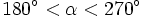
- Un ángulo
 , pertenece al cuarto cuadrante si
, pertenece al cuarto cuadrante si 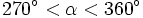
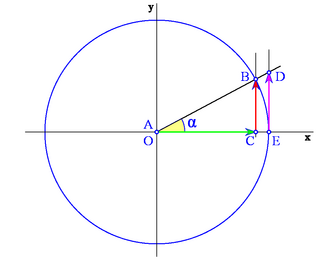
Según en qué cuadrante estemos, el segmento OC que determina al coseno, puede estar situado a la derecha o a la izquierda del origen O. Así, asignaremos signo positivo al coseno si está a la derecha de O y negativo si está a la izquierda.
Analogamente, el segmento CB que determina al seno, puede estar situado por encima o por debajo del eje X . Asignaremos signo positivo al seno si está por encima y negativo si está por debajo.
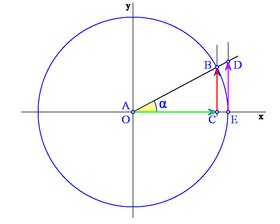
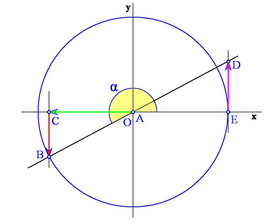
Los siguientes gráficos muestran los distintos casos según en qué cuadrante se encuentre el ángulo:
En esta escena podrás ver como se representan las razones trigonométricas de un ángulo de cualquier cuadrante.
En esta escena podrás ver los valores y el signo de las 6 razones trigonométricas de un ángulo de cualquier cuadrante.
Si el lado origen de un ángulo orientado es el semieje OX, del cuadrante en que está el lado extremo se dice "cuadrante del ángulo". En este video definimos las razones trigonométricas de un ángulo orientado, y para ello empleamos las coordenadas de un punto cualquiera (a;b) del lado extremo.
3 ejercicios sobre razones trigonométricas de ángulos orientados.
Si -1 < a < 1, en el primer giro hay dos ángulos cuyo seno es "a". Si -1 < b < 1, en el primer giro hay dos ángulos cuyo coseno es "b". Si "c" es un número real, en el primer giro hay dos ángulos cuyo tangente es "c".
En este vídeo empleamos la calculadora científica para determinar los dos ángulos del primer giro cuyo seno es 0.3 y los dos ángulos del primer giro cuyo seno es -0.4.
Relaciones fundamentales de la trigonometría (ángulos de cualquier cuadrante)
Las relaciones fundamentales de la trigonometría, ya estudiadas anteriormente, siguen siendo válidas con las definiciones dadas para ángulos de cualquier cuadrante.
Practica con las relaciones fundamentales de la trigonometría y ponte a prueba con una autoevaluación. En estas actividades tendrás que tener en cuenta en qué cuadrante está el ángulo para determinar el signo de la razón trigonométrica.
- Si pulsas el botón "EJERCICIO" cambiarán los datos del problema.
- Si pulsas el botón "AUTOEVALUACIÓN" podrás realizar una tanda de ejercicios para comprobar lo que sabes.
|
Actividad: Razones trigonométricas de ángulos cualesquiera
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Ejercicios propuestos
|
Ejercicios propuestos: Razones trigonométricas de ángulos cualesquiera |
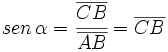
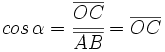
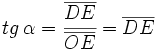


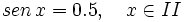 (2º cuadrante)
(2º cuadrante)
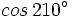
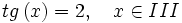 (3º cuadrante), halla
(3º cuadrante), halla 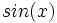 .
.

