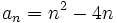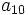Concepto de sucesión (1ºBach)
De Wikipedia
| Revisión de 11:16 18 sep 2016 Coordinador (Discusión | contribuciones) (→Término general de una sucesión) ← Ir a diferencia anterior |
Revisión de 11:16 18 sep 2016 Coordinador (Discusión | contribuciones) (→Ejercicios propuestos) Ir a siguiente diferencia → |
||
| Línea 79: | Línea 79: | ||
| |cuerpo= | |cuerpo= | ||
| - | :(Pág. 57) | + | (Pág. 57) |
| - | :[[Imagen:yellow_star.png|12px]] 1 | + | [[Imagen:yellow_star.png|12px]] 1 |
| - | :[[Imagen:red_star.png|12px]] 2 | + | [[Imagen:red_star.png|12px]] 2 |
| }} | }} | ||
| [[Categoría: Matemáticas|Sucesiones]][[Categoría: Números|Sucesiones]] | [[Categoría: Matemáticas|Sucesiones]][[Categoría: Números|Sucesiones]] | ||
Revisión de 11:16 18 sep 2016
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
Sucesión de números reales
(pág. 56)
Una sucesión de números reales es una función,  , que a cada número natural,
, que a cada número natural,  , le asocia un único número real,
, le asocia un único número real, 
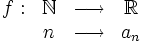
Esto genera el conjunto ordenado
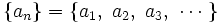
de los términos de la sucesión.
Se suele identificar a la sucesión con sus términos. Normalmente hablaremos de la sucesión de términos 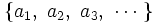 en lugar de la sucesión
en lugar de la sucesión  .
.
Los términos de una sucesión pueden seguir un cierto criterio:
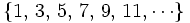 . Sus términos son los números impares.
. Sus términos son los números impares.
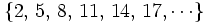 . Sus términos se obtienen sumando 3 al anterior.
. Sus términos se obtienen sumando 3 al anterior.
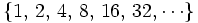 . Sus términos son las potencias de 2.
. Sus términos son las potencias de 2.
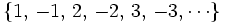 . Sus términos van ascendiendo y alternando el signo.
. Sus términos van ascendiendo y alternando el signo.
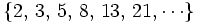 . Sus términos, a partir del tercero, se obtienen sumando los dos anteriores.
. Sus términos, a partir del tercero, se obtienen sumando los dos anteriores.
o no seguir ninguno:
- Tutorial en el que se introducen los conceptos básicos de las sucesiones numéricas.
- (05:20): Definiciones básicas (sucesión, términos e índices) y ejemplo inicial.
Actividades en las que aprenderás a obtener los términos de una sucesión a partir de una regla de formación dada.
Término general de una sucesión
Se llama término general de una sucesión, y se simboliza por  , a la expresión que representa a uno cualquiera de sus términos. La sucesión correspondiente se representa de forma abreviada por
, a la expresión que representa a uno cualquiera de sus términos. La sucesión correspondiente se representa de forma abreviada por 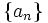
- Hay veces que el término general se puede expresar mediante una fórmula:
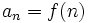 . Dándole a
. Dándole a  un valor, se obtiene el término correspondiente.
un valor, se obtiene el término correspondiente.
- Otras veces, cada término de la sucesión se obtiene a partir de operaciones con otros términos anteriores. A estas sucesiones se les llama recurrentes. En ellas, para hallar un término, tenemos que hallar todos los anteriores. En estos casos se suele dar una ley de recurrencia, una regla que relaciona cada término con sus anteriores.
- La sucesión,
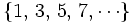 , de los números impares, tiene como término general:
, de los números impares, tiene como término general:
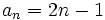
- En efecto, dándole valores a n, se obtienen sus términos:
- etc.
- Esta misma sucesión también se podría definir mediante la siguiente ley de recurrencia:
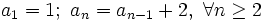
- En efecto, dándole valores a n, se obtienen sus términos:
- etc.
Sucesiones con término general:
- Sucesión.
- Término general de una sucesión.
- Cálculo de una sucesión a partir de sus término general.
- Ejemplos.
Tutorial en el que se explica y trabajan los términos generales en las sucesiones numéricas.
Sucesiones y término general.
- Definición de sucesión de números reales como aplicación entre el conjunto de los números naturales y el de los números reales.
- Término general de una sucesión.
Ejemplos de sucesiones con figuras.
Sucesiones recurrentes:
- Sucesiones recurrentes.
- Cálculo de los términos de una sucesión recurrente.
- Ejemplos.
Tutorial en el que se explica y trabajan las leyes de recurrencia en las sucesiones numéricas.
Definición de sucesiones de manera explicita y recursiva.
Calcula los cuatro primeros términos de sucesiones dadas de forma recurrente:
- a)
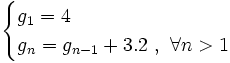
- b)
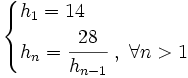
- c)
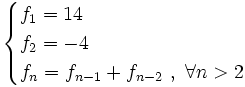
Actividades en las que aprenderás el concepto de término general de una sucesión y a obtener, a partir de él, los términos de la misma.
Evalúa sucesiones a partir de una ley de recurrencia.
|
Actividad: Termino general de una sucesión
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
(pág. 57)
Ejercicios resueltos: Concepto de sucesión
Descubre el criterio por el que se forman las sucesiones siguientes, añadir dos nuevos términos a cada una y dar su término general o la ley de recurrencia:
- a)
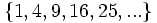 b)
b) 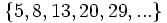 c)
c) 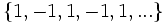 d)
d) 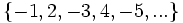
- e)
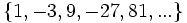 f)
f) 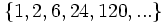 g)
g) 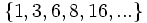
a) Son los cuadrados de los números naturales
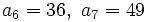
- Término general:
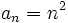
b) Cada término es cuatro unidades mayor que el correspondiente de la sucesión del apartado a)
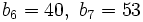
- Término general:
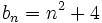
c) Los términos impares valen 1 y los pares -1.
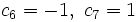
- Término general:
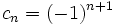
d) Los términos son los números naturales con los signos alternando: pares positivos e impares negativos.
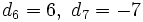
- Término general:
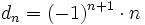
e) Cada término se obtiene multiplicando el anterior por -3.
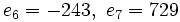
- Término general:
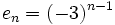
f) Cada término se obtiene multiplicando el anterior por el número del lugar que ocupa.
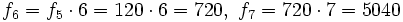
- La ley de recurrencia es
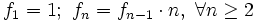
- También se puede dar un término general:
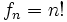
g) Los términos pares se obtiene sumando 2 al anterior y los impares, apartir del tercero, multiplicando por 2 el anterior.
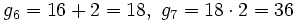
- La ley de recurrencia es
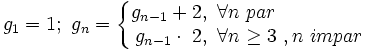
Tipos de sucesiones
Sucesiones monótonas
Una sucesión es monótona si es de alguno de estos cuatro tipos:
- Estrictamente creciente: Una sucesión es estrictamente creciente si cada término es mayor que el anterior.
- Estrictamente decreciente: Una sucesión es estrictamente decreciente si cada término de la sucesión es menor que el anterior.
- Creciente: Una sucesión es creciente si cada término es mayor o igual que el anterior.
- Decreciente: Una sucesión es decreciente si cada término de la sucesión es menor o igual que el anterior.
Sucesiones constantes
Una sucesión es constante si todos sus términos son iguales.
Sucesiones acotadas
- Sucesión acotada inferiormente: Es aquella en la que todos sus términos son mayores o iguales que un cierto número K, que llamaremos cota inferior de la sucesión.
- Sucesión acotada superiormente: Es aquella en la que todos sus términos son menores o iguales que un cierto número K, que llamaremos cota superior de la sucesión.
- Sucesión acotada: Es aquella en la que está acotada superior e inferiormente.
Ejercicios propuestos
|
Ejercicios propuestos: Término general de una sucesión |
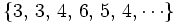
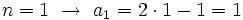
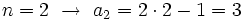
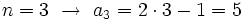
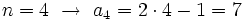
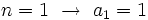
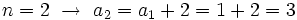
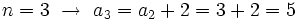
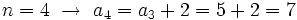
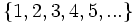 b)
b) 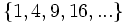 c)
c) 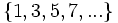
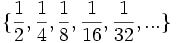 e)
e) 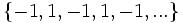 f)
f)