Fracciones equivalentes (1º ESO)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 10:05 24 sep 2016 Coordinador (Discusión | contribuciones) (→Obtención de fracciones equivalentes) ← Ir a diferencia anterior |
Revisión de 10:14 24 sep 2016 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 58: | Línea 58: | ||
| :<math>\cfrac{24}{30} = \cfrac{4}{5}</math> | :<math>\cfrac{24}{30} = \cfrac{4}{5}</math> | ||
| }} | }} | ||
| - | + | {{p}} | |
| ===Ejercicios propuestos=== | ===Ejercicios propuestos=== | ||
| {{ejercicio | {{ejercicio | ||
| Línea 75: | Línea 75: | ||
| ==Relación entre los términos de dos fracciones equivalentes== | ==Relación entre los términos de dos fracciones equivalentes== | ||
| ===Cómo averiguar si dos fracciones son equivalentes=== | ===Cómo averiguar si dos fracciones son equivalentes=== | ||
| + | {{Teorema_sin_demo|titulo=Procedimiento|enunciado=Para averiguar si dos fracciones son equivalentes comprobaremos si los productos cruzados de sus términos son iguales. | ||
| + | {{p}} | ||
| + | <center><math>\cfrac{a}{b} = \cfrac{c}{d} \iff a \cdot d = b \cdot c</math></center> | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Ejemplo_simple|titulo=Ejemplo:|contenido= | ||
| + | <math>\cfrac{4}{3} = \cfrac{12}{9}</math> porque <math>4 \cdot 9 = 3 \cdot 12 = 36</math> (son equivalentes) | ||
| + | |||
| + | <math>\cfrac{6}{5} \ne \cfrac{12}{4}</math> porque <math>6 \cdot 4 = 24 \ne 5 \cdot 12 = 60</math> (no son equivalentes) | ||
| + | |||
| + | }} | ||
| ===Cómo averiguar el término que falta en una igualdad entre fracciones=== | ===Cómo averiguar el término que falta en una igualdad entre fracciones=== | ||
Revisión de 10:14 24 sep 2016
Menú:
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
(Pág. 125)
Fracciones equivalentes
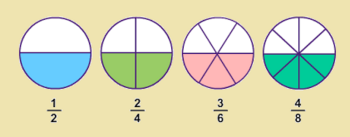
Dos fracciones son equivalentes si tienen el mismo valor. En la Fig.1 tienes ejemplos de fracciones equivalentes. Fíjate como representan la misma porción de la unidad aunque sus numeradores y denominadores sean diferentes. |
Obtención de fracciones equivalentes
Procedimiento
Si se multiplica o se divide el numerador y el denominador de una fracción por un mismo número, se obtiene una fracción equivalente.
Simplificación de fracciones
- Simplificar una fracción es sustituirla por otra equivalente con los términos más pequeños.
- Cuando una fracción no se puede simplificar se dice que es irreducible.
Procedimiento
- Para simplificar fracciones se divide numerador y denominador por un mismo número.
- Si queremos simplificar hasta hacer la fracción irreducible debemos dividir numerador y denominador por el m.c.d. de ambos.
Simplifica 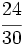 :
:
Solución:
- Paso a paso: Dividimos por 2 y luego por 3
- En un solo paso: Calculamos el m.c.d.(24,30) = 6, y dividimos directamente por 6:
Ejercicios propuestos
|
Ejercicios propuestos: Fracciones equivalentes |
Relación entre los términos de dos fracciones equivalentes
Cómo averiguar si dos fracciones son equivalentes
Procedimiento
Para averiguar si dos fracciones son equivalentes comprobaremos si los productos cruzados de sus términos son iguales.
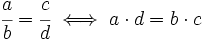
Cómo averiguar el término que falta en una igualdad entre fracciones
Ejercicios propuestos
|
Ejercicios propuestos: Relación entre los términos de dos fracciones equivalentes |
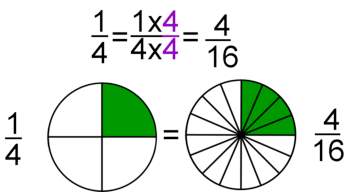
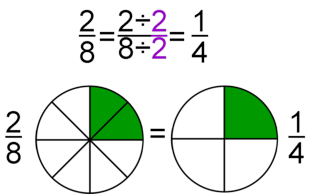
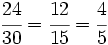
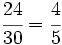
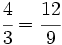 porque
porque 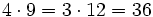 (son equivalentes)
(son equivalentes)
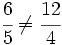 porque
porque 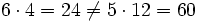 (no son equivalentes)
(no son equivalentes)

