Problemas de proporcionalidad inversa (1º ESO)
De Wikipedia
| Revisión de 12:57 28 sep 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 12:59 28 sep 2016 Coordinador (Discusión | contribuciones) (→Regla de tres inversa) Ir a siguiente diferencia → |
||
| Línea 36: | Línea 36: | ||
| {{p}} | {{p}} | ||
| ==Regla de tres inversa== | ==Regla de tres inversa== | ||
| + | {{p}}{{Teorema_sin_demo|titulo=Procedimiento|enunciado=La '''regla de tres inversa''' es un método que se apoya en el hecho de que al multiplicar dos magnitudes directamente proporcionales el producto no varía. Esto permite establecer una ecuación de la cual se obtiene el valor desconocido.}} | ||
| {{p}} | {{p}} | ||
| + | {{Ejemplo_simple|titulo=Ejemplo:|contenido= | ||
| + | Compramos 4 kg de plátanos por 6 €. ¿Cuánto costarán 7 kg? | ||
| + | ---- | ||
| + | '''Solución:''' | ||
| + | |||
| + | Peso (kg) Coste (€) | ||
| + | ---------- ---------- | ||
| + | 4 --------> 6 | ||
| + | 7 --------> x | ||
| + | |||
| + | :<math>\cfrac{6}{4} = \cfrac{x}{7} \ \rightarrow \ 6 \cdot 7 = 4 \cdot x \ \rightarrow \ x = \cfrac{6 \cdot 7}{4} = 10.5</math> € | ||
| + | |||
| + | }} | ||
| + | {{p}} | ||
| + | |||
| ==Actividades== | ==Actividades== | ||
| {{AI_enlace|titulo1=Actividades: ''Problemas de proporcionalidad inversa'' | {{AI_enlace|titulo1=Actividades: ''Problemas de proporcionalidad inversa'' | ||
Revisión de 12:59 28 sep 2016
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
(Pág. 156)
Método de reducción a la unidad
Procedimiento
El método de reducción a la unidad consiste en averiguar el valor la segunda magnitud si la primera vale 1 (la unidad). A partir de esa información, es fácil sacar los demás valores de la segunda magnitud a partir de los de la primera, ya que sólo tendremos que dividir la primera magnitud por dicho valor.
Dos grifos tardan en llenar una piscina en 6 horas. ¿Cuánto tiempo taradarán 3 grifos?
Solución:
Primero averiguamos lo que tarda 1 grifo (la unidad):
Nº grifos Tiempo (h)
---------- ----------
2 --------> 6
1 --------> x
- No se pudo entender (función desconocida\dcot): x=6 \dcot 2 = 12
h
A partir del tiempo que tarda 1 grifo es fácil sacar el que tardan 3 grifos:
Nº grifos Tiempo (h)
---------- ----------
1 --------> 12
3 --------> x
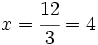h
Regla de tres inversa
Procedimiento
La regla de tres inversa es un método que se apoya en el hecho de que al multiplicar dos magnitudes directamente proporcionales el producto no varía. Esto permite establecer una ecuación de la cual se obtiene el valor desconocido.
Compramos 4 kg de plátanos por 6 €. ¿Cuánto costarán 7 kg?
Solución:
Peso (kg) Coste (€)
---------- ----------
4 --------> 6
7 --------> x
€
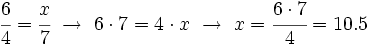Actividades
Actividades: Problemas de proporcionalidad inversa Descripción: Ejercicios propuestos
 Ejercicios propuestos: Problemas de proporcionalidad inversa (Pág. 157)
|
