Plantilla:Cálculo de los divisores de un número

De Wikipedia

(Diferencia entre revisiones)

Saltar a navegación, búsqueda

Revisión de 10:18 20 oct 2016

Propiedades

Todo número natural tiene una cantidad finita de divisores.
Todo número natural tiene, al menos, dos divisores: 1 y él mismo.
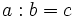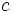Para encontar todos los divisores de un número, $a\,$ , buscamos las divisiones exactas $a:b=c\,$ . Entonces $b\,$ y $c\,$ son divisores de $a\,$ . Para ello procederemos de la siguiente manera:

Probaremos con $b = 1, 2, 3, ... \,$ .
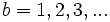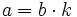Para cada valor de $b\,$ que dé división exacta ( $a= b \cdot k$ ), tendremos dos divisores: $b\,$ y $k\,$ .
Pararemos de probar cuando el cociente de la división 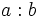$a:b\,$ sea menor o igual que $b\,$ .

Ejercicio resuelto: Cálculo de los divisores de un número

2. Calcula los divisores de 44.

Solución:

44 : 1 = 44 $\rightarrow$ 1 y 44 son divisores. Sigo porque 44 > 1

44 :2 = 22 $\rightarrow$ 2 y 22 son divisores. Sigo porque 22 > 2

44 : 3 $\rightarrow$ No es exacta (cociente=14). Sigo porque 14 > 3

44 : 4 = 11 $\rightarrow$ 4 y 11 son divisores. Sigo porque 11 > 4

44 : 5 $\rightarrow$ No es exacta (cociente=8). Sigo porque 8 > 5

44 : 6 $\rightarrow$ No es exacta (cociente=7). Sigo porque 7 > 6

44 : 7 $\rightarrow$ No es exacta (cociente=6). Paro porque 6 < 7

Solución: Tenemos 6 divisores de 44: 1, 2, 4, 11, 22 y 44.

Múltiplos y divisores

Actividad: Múltiplos y divisores de un número

a) Halla los divisores de 70.

b) Halla 5 múltiplos de 6.

c) Halla 5 múltiplos comunes de 4 y 5.

d) ¿Es 5 divisible por 10?

Solución:

Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:

a) divisors 70

b) multiples 6

c) common multiples 4,5

d) is 5 divisible by 10?

Separa los divisores de un número de los que no lo son Descripción:

Busca los números de abajo que sean divisores del número de arriba y colócalos en el rectángulo de la izquierda. En el rectángulo de la derecha coloca los números que no sean sus divisores.

Busca los divisores de un número Descripción:

Cada número natural tiene una cantidad concreta de divisores, solamente el número 0 tiene infinitos divisores.

Busca los divisores del número que aparezca y márcalos de uno en uno en la ventana del control inferior. Cada vez que marques un divisor debes pulsar intro. Cuando hayas marcado todos sus divisores sin errores aparecerá el mensaje ENHORABUENA.

Cada vez que pulses sobre inicio aparecerá aleatoriamente otro número de dos cifras.

Calcula los divisores de un número Descripción:

Marca el número que quieras en la ventana del control que está bajo la escena y pulsa intro, así aparecerán todos los divisores que tiene ese número.

También puedes ir variando el valor del número utilizando los triángulos arriba y abajo. El número más grande que puedes marcar es el 10.000

Investiga y contesta en tu cuaderno:

Toma nota de la cantidad de divisores de cada uno de los números del 0 al 50

a) ¿Cuál es el número natural que tiene mayor cantidad de divisores? ¿Cuántos divisores tiene?

b) ¿Cuál es el número natural que tiene menor cantidad de divisores? ¿Cuántos divisores tiene?

c) ¿Cuántos divisores tiene un número primo?

Marca un número de 4 cifras, pulsa intro, con el triángulo arriba vete aumentando de uno en uno el valor del número. Observa la disparidad de número de divisores que tiene cada número. Anota lo que observes.

d) ¿Crees que un número grande es de esperar necesariamente que tenga más divisores?

e) ¿De qué crees que depende?

Juego de los múltiplos y divisores Descripción:

Normas del juego:

Es un juego de competición entre dos jugadores.
Cada jugador retira por turno un número sacándolo de la escena.
Los números retirados ya no se reponen.
El número que se retira debe ser múltiplo o divisor del retirado anteriormente y que figura en el recuadro.
Pierde el jugador que retire un número indebido o el que ya no pueda retirar un número.
Para no dar ventaja al primer jugador, se exige que el primer número retirado sea par.

Obtenido de "http://maralboran.org/wikipedia/index.php/Plantilla:C%C3%A1lculo_de_los_divisores_de_un_n%C3%BAmero"

 *Todo número natural tiene, al menos, dos divisores: 1 y él mismo.
 *Para encontar todos los divisores de un número, <math>a\,</math>, buscamos las divisiones exactas {{Sube|porcentaje=15%|contenido=<math>a:b=c\,</math>}}. Entonces {{Sube|porcentaje=15%|contenido=<math>b\,</math>}} y <math>c\,</math> son divisores de <math>a\,</math>. Para ello procederemos de la siguiente manera:
-:#Probaremos con <math>b = 1, 2, 3, ... \,</math>.
+#Probaremos con <math>b = 1, 2, 3, ... \,</math>.
-:#Para cada valor de {{Sube|porcentaje=15%|contenido=<math>b\,</math>}} que dé división exacta ({{Sube|porcentaje=20%|contenido=<math>a= b \cdot k</math>}}), tendremos dos divisores: {{Sube|porcentaje=15%|contenido=<math>b\,</math>}} y {{Sube|porcentaje=15%|contenido=<math>k\,</math>}}.
+#Para cada valor de {{Sube|porcentaje=15%|contenido=<math>b\,</math>}} que dé división exacta ({{Sube|porcentaje=20%|contenido=<math>a= b \cdot k</math>}}), tendremos dos divisores: {{Sube|porcentaje=15%|contenido=<math>b\,</math>}} y {{Sube|porcentaje=15%|contenido=<math>k\,</math>}}.
-:#Pararemos de probar cuando el cociente de la división {{Sube|porcentaje=15%|contenido=<math>a:b\,</math>}} sea menor o igual que {{Sube|porcentaje=15%|contenido=<math>b\,</math>}}.
+#Pararemos de probar cuando el cociente de la división {{Sube|porcentaje=15%|contenido=<math>a:b\,</math>}} sea menor o igual que {{Sube|porcentaje=15%|contenido=<math>b\,</math>}}.
 }}
 {{p}}
 |titulo=Ejercicio resuelto: ''Cálculo de los divisores de un número''
 |enunciado=
-:'''2.''' Calcula los divisores de 44.
+'''2.''' Calcula los divisores de 44.
 |sol=
-:44 : 1 = 44 <math>\rightarrow</math> '''1''' y '''44''' son divisores. Sigo porque 44 > 1
+: 1 = 44 <math>\rightarrow</math> '''1''' y '''44''' son divisores. Sigo porque 44 > 1
-:44 :2 = 22 <math> \rightarrow</math>  '''2''' y '''22''' son divisores. Sigo porque 22 > 2
-:44 : 3 <math> \rightarrow</math> No es exacta (cociente=14). Sigo porque 14 > 3
-:44 : 4 = 11 <math> \rightarrow</math>  '''4''' y '''11''' son divisores. Sigo porque 11 > 4
-:44 : 5 <math> \rightarrow</math> No es exacta (cociente=8). Sigo porque 8 > 5
-:44 : 6 <math> \rightarrow</math> No es exacta (cociente=7). Sigo porque 7 > 6
-:44 : 7 <math> \rightarrow</math> No es exacta (cociente=6). Paro porque 6 < 7
-:'''Solución:''' Tenemos 6 divisores de 44: 1, 2, 4, 11, 22 y 44.
+:2 = 22 <math> \rightarrow</math>  '''2''' y '''22''' son divisores. Sigo porque 22 > 2
+: 3 <math> \rightarrow</math> No es exacta (cociente=14). Sigo porque 14 > 3
+: 4 = 11 <math> \rightarrow</math>  '''4''' y '''11''' son divisores. Sigo porque 11 > 4
+: 5 <math> \rightarrow</math> No es exacta (cociente=8). Sigo porque 8 > 5
+: 6 <math> \rightarrow</math> No es exacta (cociente=7). Sigo porque 7 > 6
+: 7 <math> \rightarrow</math> No es exacta (cociente=6). Paro porque 6 < 7
+'''Solución:''' Tenemos 6 divisores de 44: 1, 2, 4, 11, 22 y 44.
 }}
 {{p}}

Plantilla:Cálculo de los divisores de un número

De Wikipedia

Revisión de 10:18 20 oct 2016

Vistas

Herramientas personales

Menú

Buscar

Herramientas