Plantilla:Aproximaciones
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 17:12 20 sep 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 08:23 24 oct 2016 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 22: | Línea 22: | ||
| 263825 ---> 260000 ---> 270000 ---> 2 ---> Decenas de millar | 263825 ---> 260000 ---> 270000 ---> 2 ---> Decenas de millar | ||
| 6035192 ---> 6000000 ---> 7000000 ---> 1 ---> Unidades de millón | 6035192 ---> 6000000 ---> 7000000 ---> 1 ---> Unidades de millón | ||
| - | 60,35 ---> 60,3 ---> 60,4 ---> 3 ---> Décimas | + | 60.35 ---> 60.3 ---> 60.4 ---> 3 ---> Décimas |
| {{p}} | {{p}} | ||
| }} | }} | ||
| Línea 34: | Línea 34: | ||
| |enunciado= | |enunciado= | ||
| Redondea los siguientes números:{{p}} | Redondea los siguientes números:{{p}} | ||
| - | :a) 27640,342 a la centena. | + | :a) 27640.342 a la centena. |
| - | :b) 3857,567 a la décima. | + | :b) 3857.567 a la décima. |
| - | :c) 24572,2578 a la unidad de millar. | + | :c) 24572.2578 a la unidad de millar. |
| {{p}} | {{p}} | ||
| |sol= | |sol= | ||
| - | a) 27600 ; b) 3857,6 ; c) 25000 | + | a) 27600 ; b) 3857.6 ; c) 25000 |
| }} | }} | ||
| Línea 50: | Línea 50: | ||
| |enunciado= | |enunciado= | ||
| Trunca los siguientes números :{{p}} | Trunca los siguientes números :{{p}} | ||
| - | :a) 27630,24578 a la milésima. | + | :a) 27630.24578 a la milésima. |
| - | :b) 3851,34 a la unidad. | + | :b) 3851.34 a la unidad. |
| - | :c) 12345621,2 a la decena de millar. | + | :c) 12345621.2 a la decena de millar. |
| {{p}} | {{p}} | ||
| - | |sol=a) 27630,245 ; b) 3851 ; c) 12340000 | + | |sol=a) 27630.245 ; b) 3851 ; c) 12340000 |
| }} | }} | ||
Revisión de 08:23 24 oct 2016
Cuando escribimos el número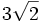 
queda reflejado con total precisión de qué número estamos hablando. Este número, tan sencillo de expresar con radicales, tiene, sin embargo, una expresión decimal que consta de infinitas cifras (4.2426406871192851464050661726291...). En la práctica, muchas veces es preferida la expresión decimal aproximada, con una cantidad reducida de cifras decimales (4.24), aunque ésta sea imprecisa, porque resulta más fácil captar su valor que expresándolo con radicales.
- Cuando un número tiene muchas cifras, es difícil recordarlo y operar con él. Por eso lo solemos sustituir por otro más manejable de valor similar, prescindiendo de sus últimas cifras. Ese otro número más sencillo decimos que es una aproximación del número de partida.
- Cuando aproximamos un número, nos quedamos con sus primeras cifras y completamos con ceros. Esas cifras, con las que nos quedamos, se llaman cifras significativas.
- Llamamos orden de la aproximación, a la posición hasta la que nos quedamos con cifras significativas.
- Se puede aproximar por defecto si el número utilizado es menor que el de partida, o por exceso si el número utilizado es mayor que el de partida.
Ejemplo: Aproximaciones
Aproxima por defecto y por exceso los siguientes números e indica el orden de la aproximación:
- a) 263825 con 2 cifras significativas.
- b) 6035192 con 1 cifra significativa.
- c) 60,35 con 3 cifras significativas.
Solución:
Número Aproximación Aproximación Nº cifras Orden de la
de partida por defecto por exceso significativas aproximación
------------ ------------ -------------- -------------- -------------------
263825 ---> 260000 ---> 270000 ---> 2 ---> Decenas de millar
6035192 ---> 6000000 ---> 7000000 ---> 1 ---> Unidades de millón
60.35 ---> 60.3 ---> 60.4 ---> 3 ---> Décimas
Redondeo
Para redondear un número a un determinado orden de unidades:
- Se sustituyen por ceros todas las cifras a la derecha de dicho orden
- Si la primera cifra sustituida es mayor o igual que cinco se suma una unidad a la cifra anterior
Ejemplo: Redondeo
Redondea los siguientes números:
- a) 27640.342 a la centena.
- b) 3857.567 a la décima.
- c) 24572.2578 a la unidad de millar.
Solución:
a) 27600 ; b) 3857.6 ; c) 25000
Truncamiento
Para truncar un número a un determinado orden de unidades se sustituyen por ceros todas las cifras a la derecha de dicho orden.
Ejemplo: Truncamiento
Trunca los siguientes números :
- a) 27630.24578 a la milésima.
- b) 3851.34 a la unidad.
- c) 12345621.2 a la decena de millar.
Solución:
a) 27630.245 ; b) 3851 ; c) 12340000
