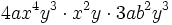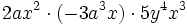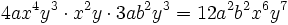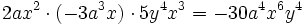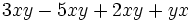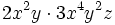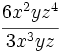Plantilla:Operaciones con monomios
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 19:01 24 oct 2016 Coordinador (Discusión | contribuciones) (→Producto de monomios) ← Ir a diferencia anterior |
Revisión de 19:01 24 oct 2016 Coordinador (Discusión | contribuciones) (→División de monomios) Ir a siguiente diferencia → |
||
| Línea 44: | Línea 44: | ||
| |titulo=Ejemplos: ''División de monomios'' | |titulo=Ejemplos: ''División de monomios'' | ||
| |enunciado= | |enunciado= | ||
| - | :Calcula: | + | Calcula: |
| + | |||
| :a) <math>4ax^4y^3 : 2x^2y \;\!</math> | :a) <math>4ax^4y^3 : 2x^2y \;\!</math> | ||
| + | |||
| :b) <math>6x^4y : 2ax^3 \;\!</math> | :b) <math>6x^4y : 2ax^3 \;\!</math> | ||
| |sol= | |sol= | ||
| - | :a) <math>4ax^4y^3 : 2x^2y = \cfrac {4ax^4y^3}{2x^2y}=2ax^2y^2</math> | + | a) <math>4ax^4y^3 : 2x^2y = \cfrac {4ax^4y^3}{2x^2y}=2ax^2y^2</math> |
| - | :b) <math>6x^4y : 2ax^3 =\cfrac {6x^4y}{2ax^3}</math>. No es posible la división pues no hay <math>a \;\!</math> en el numerador. | + | |
| + | b) <math>6x^4y : 2ax^3 =\cfrac {6x^4y}{2ax^3}</math>. No es posible la división pues no hay <math>a \;\!</math> en el numerador. | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión de 19:01 24 oct 2016
Suma y resta de monomios
Para sumar o restar dos monomios tienen que ser semejantes. La suma o resta es otro monomio semejante a ellos que tiene por coeficiente la suma o diferencia, según el caso, de los coeficientes.
Ejemplos: Suma y resta de monomios
Calcula:
- a)
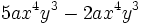
- b)
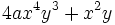
Solución:
a) 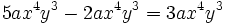
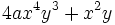 (no se pueden sumar por no ser semejantes)
(no se pueden sumar por no ser semejantes)Producto de monomios
Recordemos que para multiplicar potencias de la misma base se deja la misma base y se suman los exponentes. Así, para multiplicar monomios, se multiplican los coeficientes de cada monomio y las potencias con la misma base se agrupan y se multiplican.
División de monomios
Entenderemos la división como una fracción que hay que simplificar, dividiendo los coeficientes y restando los exponentes de las potencias de la misma base.
Ejemplos: División de monomios
Calcula:
- a)
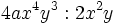
- b)
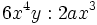
Solución:
a) 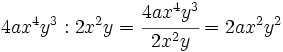
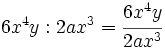 . No es posible la división pues no hay
. No es posible la división pues no hay  en el numerador.
en el numerador.