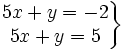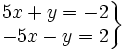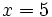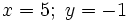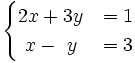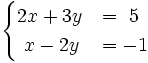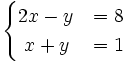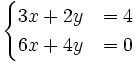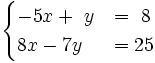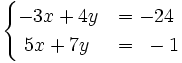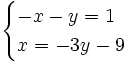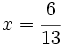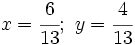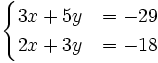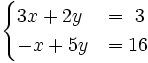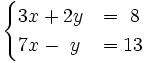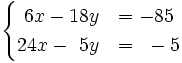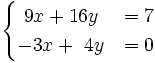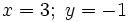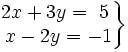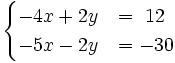Plantilla:Sistemas de ecuaciones de primer grado
De Wikipedia
| Revisión de 17:45 30 oct 2016 Coordinador (Discusión | contribuciones) (→Resolución de problemas mediante sistemas) ← Ir a diferencia anterior |
Revisión de 17:46 30 oct 2016 Coordinador (Discusión | contribuciones) (→Método de reducción) Ir a siguiente diferencia → |
||
| Línea 156: | Línea 156: | ||
| ===Método de reducción=== | ===Método de reducción=== | ||
| - | {{Caja Amarilla|texto= | + | {{Método de reducción}} |
| - | El método de '''reducción''' consiste en obtener ecuaciones equivalentes a las de partida, de manera que al sumarlas, se obtenga una ecuación en la que se ha eliminado una de las incógnitas. Así, nos queda una ecuación con una sola incógnita, que se resuelve, permitiendo averiguar dicha incógnita. Finalmente, el valor de la otra incógnita se obtiene sustituyendo el valor obtenido. | + | |
| - | }} | + | |
| - | {{p}} | + | |
| - | {{Ejemplo|titulo=Ejemplo: ''Método de reducción'' | + | |
| - | |enunciado= | + | |
| - | :Resuelve por el método de reducción el siguiente sistema: | + | |
| - | <center><math>\left . \begin{matrix} 3x+2y=7 \\ 4x-3y=15 \end{matrix} \right \}</math></center> | + | |
| - | |sol= | + | |
| - | *Multiplicamos la primera ecuación por 4 y la segunda por (-3) | + | |
| - | <center><math>\left . \begin{matrix} 12x+8y=28 \\ -12x+9y=-45 \end{matrix} \right \}</math></center> | + | |
| - | Sumamos miembro a miembro las dos ecuaciones: | + | |
| - | + | ||
| - | 12x + 8y = 28 | + | |
| - | -12x + 9y = -45 | + | |
| - | ---------------- | + | |
| - | 17y = -17 | + | |
| - | + | ||
| - | <center><math>y=\cfrac{-17}{17}</math></center> | + | |
| - | {{p}} | + | |
| - | {{Caja|contenido=<math>y=-1\;\!</math>}} | + | |
| - | {{p}} | + | |
| - | *Sustituimos el valor <math>y=-1\;\!</math> en cualquiera de las dos ecuaciones, por ejemplo en la primera: <math>3x+2y=7 \;\!</math> | + | |
| - | + | ||
| - | <center><math>3x+2(-1)=7 \;\!</math></center> | + | |
| - | {{p}} | + | |
| - | <center><math>3x=7+2 \;\!</math></center> | + | |
| - | {{p}} | + | |
| - | {{Caja|contenido=<math>x=3\;\!</math>}} | + | |
| - | + | ||
| - | *Así, la solución del sistema es: | + | |
| - | {{Caja|contenido=<math>x=3; \ y=-1\;\!</math>}} | + | |
| - | + | ||
| - | Comprueba en la siguiente escena la solución del sistema. para ello deberás introducir los coeficientes de cada ecuación en las casillas correspondientes. | + | |
| - | + | ||
| - | <center><iframe> | + | |
| - | url=http://maralboran.org/web_ma/descartes/Algebra/Sistemas_ecuaciones_lineales/sistema_1.html | + | |
| - | width=450 | + | |
| - | height=340 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | <center>[http://maralboran.org/web_ma/descartes/Algebra/Sistemas_ecuaciones_lineales/sistema_1.html '''Click''' aquí si no se ve bien la escena]</center> | + | |
| - | + | ||
| - | }} | + | |
Revisión de 17:46 30 oct 2016
Tabla de contenidos |
Sistemas de ecuaciones lineales 2x2
- Un sistema de dos ecuaciones de primer grado con dos incógnitas o simplemente, sistema 2x2 de ecuaciones lineales, es la agrupación de dos ecuaciones de primer grado con dos incógnitas:
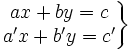
- Se llama solución de un sistema 2x2, a cualquier pareja de valores
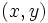que sea solución de ambas ecuaciones a la vez. Las soluciones de este tipo de sistemas son los puntos de corte de las rectas que representan cada una de las ecuaciones del sistema.
Ejemplo: Solución de un sistema de ecuaciones
Comprueba si las parejas de números (1,2) y (-1,3) son o no soluciones del sistema:
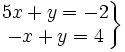
- Para comprobar si (1,2) es solución, sustituimos x=1 e y=2 en las dos ecuaciones del sistema:
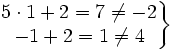
Como no se verifican las dos ecuaciones, la pareja (1,2) no es solución del sistema.
- Para comprobar si (-1,3) es solución, sustituimos x=-1 e y=3 en las dos ecuaciones del sistema:
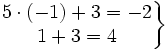
Autoevaluación 1 Descripción: Ejercicios de autoevaluación sobre sistemas de ecuaciones lineales.
Autoevaluación 2 Descripción: Comprueba soluciones de sistemas de ecuaciones lineales.
Sistemas equivalentes
Dos sistemas son equivalentes cuando tienen las mismas soluciones.
Actividad Interactiva: Sistemas equivalentes
Actividad 1: Obteniendo sistemas equivalentes.
Actividad: Dado el siguiente sistema 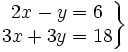 a) Represéntalo gráficamente. b) Multiplica la primera ecuación por 3 y divide la segunda por 3. Representa el nuevo sistema. c) Resta a la 2ª ecuación la 1ª ecuación y representa sobre la gráfica anterior la nueva ecuación. d) Suma a la 1ª ecuación la 2ª multiplicada por 5 y representa la nueva ecuación en la gráfica anterior. e) Comprueba el proceso en la siguiente escena: |
Número de soluciones de un sistema
- Un sistema es compatible si tiene solución e incompatible si no la tiene.
- Un sistema es determinado si tiene un número finito de soluciones e indeterminado si tiene infinitas soluciones.
- Usaremos las siguientes siglas para abreviar:
- S.C.D. : Sistema Compatible Determinado (un número finito de soluciones)
- S.C.I. : Sistema Compatible Indeterminado (infinitas soluciones)
- S.I. : Sistema Incompatible (sin solución)
Número de soluciones de un sistema 2x2 de ecuaciones lineales
Un sistema 2x2 de ecuaciones lineales puede ser:
- Compatible determinado (S.C.D.): 1 solución
- Compatible indeterminado (S.C.I.): Infinitas soluciones.
- Incompatible (S.I): 0 soluciones.
En efecto, razonando a partir de sus representaciones gráficas:
- Si las dos rectas se cortan en un punto: 1 solución (S.C.D.)
- Si las dos rectas son coincidentes: Infinitas soluciones (S.C.I.)
- Si las rectas son paralelas: 0 soluciones (S.I.)
En la siguiente actividad veremos un ejemplo de cada uno de los tres casos anteriores.
Actividad Interactiva: Soluciones de un sistema
Actividad 1: Sistema incompatible.
Actividad: Dado el siguiente sistema 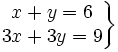 a) Represéntalo gráficamente b) ¿Cómo son las rectas que aparecen? c) ¿Existe algún punto que pertenezca a ambas rectas? d) ¿Cuantas soluciones tiene el sistema? e) Utiliza la escena para comprobar los resultados:
Actividad 2: Sistema compatible indeterminado.
Actividad: Dado el siguiente sistema 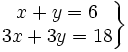 a) Represéntalo gráficamente b) ¿Cómo son las rectas que aparecen? c) ¿Existe algún punto que pertenezca a ambas rectas? d) ¿Cuantas soluciones tiene el sistema? e) Utiliza la escena para comprobar los resultados:
Actividad 3: Sistema compatible determinado.
Actividad: Dado el siguiente sistema 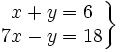 a) Represéntalo gráficamente b) ¿Cómo son las rectas que aparecen? c) ¿Existe algún punto que pertenezca a ambas rectas? d) ¿Cuantas soluciones tiene el sistema? e) Utiliza la escena para comprobar los resultados: |
Métodos de resolución de sistemas
Vamos a ver cuatro métodos para resolver un sistema de ecuaciones: Uno gráfico y tres algebraicos (sustitución, igualación y reducción).
Método grafico
Procedimiento
Para resolver un sistema de ecuaciones lineales, representaremos gráficamente las rectas de las soluciones de cada una de las ecuaciones:
- Si las rectas se cortan, el punto de corte será la única solución del sistema.
- Si las rectas son paralelas, el sistema no tendrá solución.
- Si las rectas son coincidentes, el sistema tendrá infinitas soluciones.
Tutorial 1 (8'05") Sinopsis:Resolución de sistemas por el método grafico. Ejemplos.
Tutorial 2 (25'23") Sinopsis:Tutorial en el que se muestra la resolución de sistemas de ecuaciones lineales (grado 1) de dos variables por el método gráfico.
- 00:00 a 01:50: Definiciones iniciales.
- 01:50 a 15:10: Explicación del método gráfico. Ejemplo 1.
- 15:10 a 18:40: Ejemplo 2.
- 18:40 a 22:30: Explicación de los distintos tipos de sistema en función a sus soluciones. Ejemplos 3-4-5.
- 22:30 a Fin: Utilización de la aplicación online DESMOS para la resolución de sistemas de ecuaciones.
Ejercicio 1 (10'23") Sinopsis:Resuelve gráficamente:
Ejercicio 2 (10'35") Sinopsis: Resuelve gráficamente:
Ejercicio 3 (8'02") Sinopsis: Resuelve gráficamente:
Ejercicio 4 (5'45") Sinopsis: Resuelve gráficamente:
Ejercicio 5 (3'20") Sinopsis: Resuelve gráficamente:
Ejercicio 6 (9'53") Sinopsis: 1) Resuelve gráficamente:
2) Dada la gráfica (ver video), obtén la solución aproximada del sistema.
3) Resuelve gráficamente:
Actividad 1 Descripción: - Actividad en la que aprenderás a resolver gráficamente un sistema de ecuaciones lineales con dos incógnitas.
- Actividad en la que deberás comprobar si una pareja de números son o no solución de un sistema.
Actividad 2 Descripción: Escena en la que podrás representar graficamente un sistema lineal 2x2 y resolverlo gráficamente.
Autoevaluación Descripción: Resolución de sistemas de ecuaciones por medio de gráficas.
Actividad: Método grafico de resolución de sistemas lineales 2x2 Resuelve los siguientes sistemas por el método gráfico:
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Método de sustitución
Procedimiento
Para resolver un sistema por el método de sustitución se siguen los siguientes pasos:
- Se despeja una incógnita en una de las ecuaciones (la que resulte más fácil de despejar).
- Se sustituye la incógnita despejada en (1) en la otra ecuación, obteniendo una ecuación con una sola incógnita.
- Se resuelve la ecuación obtenida en (2), averiguando así una de las incógnitas del sistema.
- El valor obtenido en (3) se sustitute en la expresión de la incógnita despejada en (1), averiguando así el valor de la incógnita que faltaba, y, por tanto, resolviendo el sistema.
Ejemplo: Método de sustitución
Resuelve por el método de sustitución el siguiente sistema:
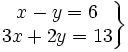
- Despejamos la
en la primera ecuación:
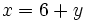[1]- Sustituimos esta expresión de la en la segunda ecuación:
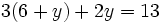
- Resolvemos la ecuación resultante:
|
|
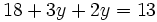
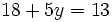
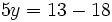
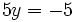
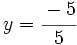
- Para obtener el valor de , sustituimos el valor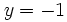
en [1]:
|
|
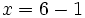
- Así, la solución del sistema es:
|
|
Tutorial 1 (0'50") Sinopsis: Método de sustitución. Ejemplo.
Tutorial 2 (9'19") Sinopsis:Método de sustitución. Ejemplos.
Tutorial 3 (16'21") Sinopsis:Tutorial en el que se muestra la resolución de sistemas de ecuaciones lineales (grado 1) de dos variables por el método de sustitución.
Ejemplos (casos sencillos) (5'39") Sinopsis: Videotutorial sobre el método de sustitución para casos sencillos.
Ejercicio 1 (7'01") Sinopsis:Resuelve por el método de sustitución:
Ejercicio 2 (3'59") Sinopsis: Resuelve por el método de sustitución:
Ejercicio 3 (4'15") Sinopsis: Resuelve por el método de sustitución:
Ejercicio 4 (4´31") Sinopsis: Resuelve por el método de sustitución:
Ejercicio 5 (11´23") Sinopsis: Resolución de sistemas lineales 2x2 por el método de sutitución:
Ejercicio 6 (5´45") Sinopsis: Resuelve por el método de sustitución:
Ejercicio 7 (6´03") Sinopsis: Resuelve por el método de sustitución:
Ejercicio 8 (8´07") Sinopsis: Resuelve por el método de sustitución:
Ejercicio 9 (7´16") Sinopsis: Resuelve por el método de sustitución:
Ejercicio 10 (7´31") Sinopsis: Resuelve por el método de sustitución:
Ejercicio 11 (5´32") Sinopsis: Resuelve por el método de sustitución:
Actividad 1 Descripción: Actividades en las que aprenderás el método de sustitución para resolver sistemas de ecuaciones lineales con dos incógnitas.
Actividad 2 Descripción: Actividades en las que aprenderás el método de sustitución para resolver sistemas de ecuaciones lineales con dos incógnitas.
Autoevaluación 1 Descripción: Resolver sistemas de ecuaciones por el método de sustitución.
Autoevaluación 2 Descripción: Ejercicios de autoevaluación sobre el método de sustitución para la resolución de sistemas de ecuaciones lineales.
Ejercicios resueltos Descripción: Ejercicios resueltos sobre el método de sustitución para la resolución de sistemas de ecuaciones lineales.
Método de igualación
Procedimiento
Para resolver un sistema por el método de igualación se siguen los siguientes pasos:
- Se despeja la misma incógnita en las dos ecuaciones del sistema.
- Se igualan las expresiones obtenidas en (1), con lo que se obtiene una ecuación con una sola incógnita.
- Se resuelve la ecuación obtenida en (2), averiguando así una de las incógnitas del sistema.
- El valor obtenido en (3) se sustitute en una de las dos expresiones de la incógnita despejada en (1), averiguando así el valor de la incógnita que faltaba, y, por tanto, resolviendo el sistema.
Ejemplo: Método de igualación
Resuelve por el método de igualación el siguiente sistema:
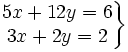
- Despejamos la en cada una de las dos ecuaciones:
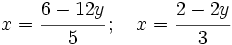[1]- Igualamos estas dos expresiones:
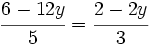
- Resolvemos la ecuación:
|
|
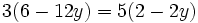
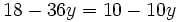
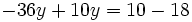
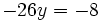
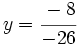
- Sustituimos el valor
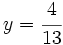en cualquiera de las expresiones de [1], por ejemplo en 
:
|
|
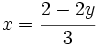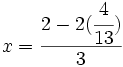
- Así, la solución del sistema es:
|
|
Tutorial 1 (0'50") Sinopsis: Método de igualación. Ejemplo.
Tutorial 2 (0'34") Sinopsis:Resolución de sistemas por igualación. Ejemplos.
Ejercicio 1 (6'52") Sinopsis:Resuelve por el método de igualación:
Ejercicio 2 (4'39") Sinopsis: Resuelve por el método de igualación:
Ejercicio 3 (5'34") Sinopsis: Resuelve por el método de igualación:
Ejercicio 4 (5´13") Sinopsis: Resuelve por el método de igualación:
Ejercicios 5 (8´10") Sinopsis: Resolución de sistemas lineales 2x2 por el método de igualación:
Ejercicio 6 (6´10") Sinopsis: Resuelve por el método de igualación:
Ejercicio 7 (7´56") Sinopsis: Resuelve por el método de igualación:
Ejercicio 8 (8´42") Sinopsis: Resuelve por el método de igualación:
Ejercicio 9 (8´56") Sinopsis: Resuelve por el método de igualación:
Ejercicio 10 (8´41") Sinopsis: Resuelve por el método de igualación:
Actividad Descripción: Actividades en las que aprenderás el método de igualación para resolver sistemas de ecuaciones lineales con dos incógnitas.
Autoevaluación Descripción: Ejercicios de autoevaluación sobre el método de igualación para la resolución de sistemas de ecuaciones lineales.
Ejercicios resueltos Descripción: Ejercicios resueltos sobre el método de igualación para la resolución de sistemas de ecuaciones lineales.
Método de reducción
Procedimiento
Para resolver un sistema por el método de reducción o eliminación se siguen los siguientes pasos:
- Se obtiene un sistema equivalente al de partida, multiplicando las dos ecuaciones por números apropiados, de manera que una de las incógnitas quede con coeficentes opuestos en ambas ecuaciones.
- Se suman las ecuaciones del nuevo sistema, desapareciendo así la incógnita con coeficientes opuestos.
- Se resuelve la ecuación obtenida en (2), averiguando así una de las incógnitas del sistema.
- El valor obtenido en (3) se sustitute en una de las dos ecuaciones del sistema de partida, averiguando así el valor de la incógnita que faltaba, y, por tanto, resolviendo el sistema.
Ejemplo: Método de reducción
Resuelve por el método de reducción el siguiente sistema:
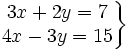
- Multiplicamos la primera ecuación por 4 y la segunda por (-3)
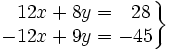
- Sumamos miembro a miembro las dos ecuaciones:
|
|
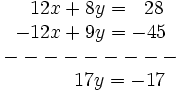
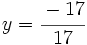
- Sustituimos el valor 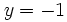en cualquiera de las dos ecuaciones del sistema de partida, por ejemplo en la primera: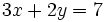
|
|
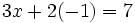
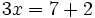
- Así, la solución del sistema es:
|
|
Tutorial 1 (0'50") Sinopsis: Método de reducción. Ejemplo.
Tutorial 2 (9'10") Sinopsis:Resolución de sistemas por reducción. Ejemplos.
Tutorial 3 (15'40") Sinopsis:Tutorial en el que se muestra la resolución de sistemas de ecuaciones lineales (grado 1) de dos variables por el método de reducción.
Ejercicio 1 (5'25") Sinopsis: Resuelve por el método de reducción:
Ejercicio 2 (7'40") Sinopsis:Resuelve por el método de reducción:
Ejercicio 3 (5'42") Sinopsis: Resuelve por el método de reducción:
Ejercicio 4 (4´14") Sinopsis: Resuelve por el método de reducción:
Ejercicio 5 (10´54") Sinopsis: Resolución de sistemas lineales 2x2 por el método de reducción:
Ejercicio 6 (7´18") Sinopsis: Resolución de sistemas lineales 2x2 por el método de reducción:
Ejercicio 7 (3'43") Sinopsis: Resuelve gráficamente:
Ejercicio 8 (6'15") Sinopsis: Resuelve gráficamente:
Ejercicio 9 (6'01") Sinopsis: Resuelve gráficamente:
Ejercicio 10 (5'30") Sinopsis: Resuelve gráficamente:
Ejercicio 11 (6'00") Sinopsis: Resuelve gráficamente:
Ejercicio 12 (6´23") Sinopsis: Resuelve por el método de reducción:
Ejercicio 13 (12´02") Sinopsis: Resuelve por el método de reducción:
- a)
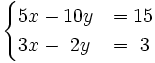
- b)
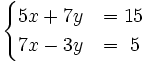
Actividad 1 Descripción: Actividades en las que aprenderás el método de reducción para resolver sistemas de ecuaciones lineales con dos incógnitas.
Actividad 2 Descripción: Actividades en las que aprenderás el método de reducción para resolver sistemas de ecuaciones lineales con dos incógnitas.
Autoevaluación 1a Descripción: Ejercicios de autoevaluación sobre el método de reducción para la resolución de sistemas de ecuaciones lineales.
Autoevaluación 1b Descripción: Ejercicios de autoevaluación sobre el método de reducción para la resolución de sistemas de ecuaciones lineales.
Autoevaluación 2 Descripción: Ejercicios de autoevaluación sobre el método de reducción para la resolución de sistemas de ecuaciones lineales.
Ejercicios resueltos Descripción: Ejercicios resueltos sobre el método de reducción para la resolución de sistemas de ecuaciones lineales.
