Plantilla:Concepto de función
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 14:26 2 nov 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 17:34 2 nov 2016 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 4: | Línea 4: | ||
| *Se dice que <math>y\;</math> '''es función''' de <math>x\;</math> y lo representamos por <math>y = f(x)\;\!</math>. También se dice que <math>y\;</math> es la '''imagen''' de <math>x\;</math> mediante la función <math>f\;</math>. | *Se dice que <math>y\;</math> '''es función''' de <math>x\;</math> y lo representamos por <math>y = f(x)\;\!</math>. También se dice que <math>y\;</math> es la '''imagen''' de <math>x\;</math> mediante la función <math>f\;</math>. | ||
| + | |||
| + | *El conjunto de valores de la variable independiente, <math>x\;</math>, para los que hay un valor de la variable dependiente, <math>y\;</math>, se llama '''dominio de definición''' de la función (Se denota <math>Dom_f\;</math>). | ||
| + | |||
| + | *El conjunto de valores que toma la variable independiente, <math>y\;</math>, se llama '''recorrido''' de la función (Se denota <math>Im_f\;</math>) | ||
| }} | }} | ||
Revisión de 17:34 2 nov 2016
- Una función es una relación entre dos variables (por ejemplo,
 e
e  ) que a cada valor de
) que a cada valor de  le asigna un único valor de
le asigna un único valor de  .
.
- La variable
 se llama variable independiente y la variable
se llama variable independiente y la variable  se llama variable dependiente, porque su valor depende de
se llama variable dependiente, porque su valor depende de  .
.
- Se dice que
 es función de
es función de  y lo representamos por
y lo representamos por 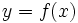 . También se dice que
. También se dice que  es la imagen de
es la imagen de  mediante la función
mediante la función  .
.
- El conjunto de valores de la variable independiente,
 , para los que hay un valor de la variable dependiente,
, para los que hay un valor de la variable dependiente,  , se llama dominio de definición de la función (Se denota
, se llama dominio de definición de la función (Se denota 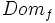 ).
).
- El conjunto de valores que toma la variable independiente,
 , se llama recorrido de la función (Se denota
, se llama recorrido de la función (Se denota 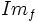 )
)

