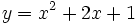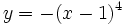Plantilla:Máximos y mínimos de una función
De Wikipedia
| Revisión de 16:53 3 nov 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 17:03 3 nov 2016 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 92: | Línea 92: | ||
| b) Pasa por el punto (0,5) y se mantiene constante en todo el intervalo [0, 8], alcanza un mínimo en (16, -1) y un máximo en (24,8). | b) Pasa por el punto (0,5) y se mantiene constante en todo el intervalo [0, 8], alcanza un mínimo en (16, -1) y un máximo en (24,8). | ||
| + | }} | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{wolfram desplegable|titulo=Máximos y mínimos|contenido= | ||
| + | {{wolfram | ||
| + | |titulo=Actividad: ''Máximos y mínimos'' | ||
| + | |cuerpo= | ||
| + | {{ejercicio_cuerpo | ||
| + | |enunciado= | ||
| + | |||
| + | Las siguientes actividades son sólo ilustrativas ya que su resolución manual excede el nivel de este curso. | ||
| + | |||
| + | :a) Halla los extremos (máximos y mínimos) de la función <math>y=x^3/3-x^2-8x\;</math>. | ||
| + | :b) Halla el mínimo de la función <math>y=x^2+2x+1\;</math> | ||
| + | :c) Halla el máximo de la función <math>y=-(x-1)^4\;</math> | ||
| + | |||
| + | {{p}} | ||
| + | |sol= | ||
| + | Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones: | ||
| + | |||
| + | :a) {{consulta|texto=extrema x^3/3-x^2-8x}} | ||
| + | :b) {{consulta|texto=minima x^2+2x+1}} | ||
| + | :c) {{consulta|texto=maxima -(x-1)^4}} | ||
| + | |||
| + | {{widget generico}} | ||
| + | }} | ||
| }} | }} | ||
| }} | }} | ||
Revisión de 17:03 3 nov 2016
- Una función
tiene un máximo relativo en un punto 
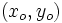cuando 
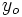es mayor que los valores que toma la variable 
en un intervalo entorno al punto. A la izquierda del máximo relativo, la función es creciente, y a su derecha, decreciente.
- Una función tiene un mínimo relativo en un punto 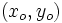cuando 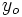es menor que los valores que toma la variable en un intervalo entorno al punto. A la izquierda del mínimo relativo, la función es decreciente, y a su derecha, creciente.
 Actividad interactiva: Crecimiento, máximos y mínimos
1. Interpreta la siguiente gráfica que muestra las temperaturas a lo largo de un día de invierno en un pueblo de Valladolid.
Actividad: La siguiente gráfica muestra las temperaturas a lo largo de un día de invierno en un pueblo de Valladolid. En el eje horizontal hemos representado las horas del día y en el eje vertical, las temperaturas. Cuando éstas aumentan decimos que la función es creciente. Cuando disminuyen, diremos que es decreciente. En aquellos puntos de la gráfica de una función donde pasa de ser decreciente a ser creciente decimos que alcanza un mínimo. En los puntos que pasa de ser creciente a ser decreciente alcanza un máximo. Haz click con el ratón en los puntos de la gráfica de los que quieras saber sus coordenadas y contesta: a) ¿Qué temperatura hizo a las 0 horas? ¿Y a las 10 horas? b) ¿A qué hora había 0º? c) ¿A qué hora se alcanzó la temperatura máxima del día?¿Cuál fue la temperatura máxima? d) ¿A qué hora se alcanzo la temperatura mínima del día? ¿Cuál fue la temperatura mínima? e) ¿En que periodo del día subió la temperatura? ¿En qué periodo bajó? ¿En qué periodos se mantuvo constante? f) ¿En qué período del día hubo una temperatura por debajo de 0º? g) Construye una tabla con las temperaturas que se registraron a lo largo del día.
2. Construye una grafica que cumpla ciertas condiciones de crecimiento, de máximos y mínimos.
Actividad: En la siguiente escena se representa la gráfica de una función creciente en el intervalo [0,8], decreciente en el intervalo [8,16] y creciente de nuevo en el intervalo [16,24]. La función alcanza un máximo en el punto B y un mínimo en el punto C. Arrastra los puntos A, B, C y D para representar gráficas con las siguientes características. En cada caso, escribe en tu cuaderno en qué intervalos la función es creciente y en cuáles es decreciente: a) Pasa por los puntos (0,3) y (24,0), alcanza un máximo en el punto (8,6), un mínimo en el punto (16,-5). b) Pasa por el punto (0,5) y se mantiene constante en todo el intervalo [0, 8], alcanza un mínimo en (16, -1) y un máximo en (24,8). |
Actividad: Máximos y mínimos Las siguientes actividades son sólo ilustrativas ya que su resolución manual excede el nivel de este curso.
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
.
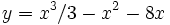