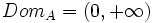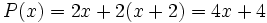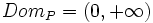Plantilla:Expresión analítica de una función
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 18:18 5 nov 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 18:20 5 nov 2016 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 16: | Línea 16: | ||
| <center><math>A(x)=x(x+2)=x^2+2x\;\!</math></center> | <center><math>A(x)=x(x+2)=x^2+2x\;\!</math></center> | ||
| {{p}} | {{p}} | ||
| - | Su dominio es: <math>Dom_A=(0,+\infty)</math> | + | Como el valor del lado, <math>x\;</math>, no puede ser un número negativo, su dominio es: <math>Dom_A=(0,+\infty)</math> |
| {{p}} | {{p}} | ||
| Línea 23: | Línea 23: | ||
| <center><math>P(x)=2x+2(x+2)=4x+4 \;\!</math> </center> | <center><math>P(x)=2x+2(x+2)=4x+4 \;\!</math> </center> | ||
| {{p}} | {{p}} | ||
| - | Su dominio es: <math>Dom_P=(0,+\infty)</math> | + | Análogamente, su dominio es: <math>Dom_P=(0,+\infty)</math> |
| |celda2=[[Imagen:rectangulo2.png]]}} | |celda2=[[Imagen:rectangulo2.png]]}} | ||
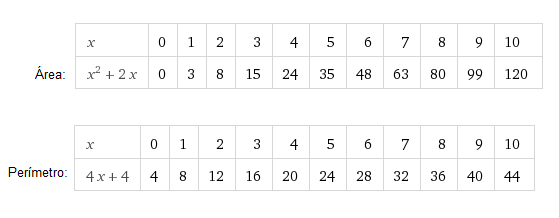
| '''3. Tablas de valores:''' | '''3. Tablas de valores:''' | ||
Revisión de 18:20 5 nov 2016
La expresión analítica de una función es una ecuación que relaciona la variable dependiente con la variable independiente.
Ejemplos: Expresión analítica de una función
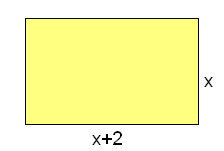
Un rectángulo mide 2 cm más de largo que de ancho.
- Halla la expresión analítica de la función que relaciona su área con su lado menor.
- Halla la expresión analítica de la función que relaciona su perímetro con su lado menor.
- Representa gráficamente las dos funciones anteriores.
Solución:
3. Tablas de valores:
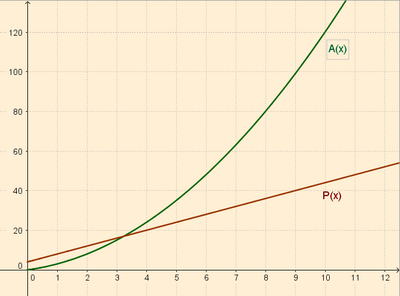
4. Representación gráfica: Realizamos una tabla de datos para cada caso. Dibujamos dichos puntos, quedando la función área como la gráfica azul y el perímetro como la gráfica verde:
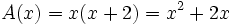
 , no puede ser un número negativo, su dominio es:
, no puede ser un número negativo, su dominio es: